Среднее
значение коэффициента нагрузки ![]() равно произведению
средних значений четырех указанных выше коэффициентов.
равно произведению
средних значений четырех указанных выше коэффициентов.
Среднее
значение коэффициента ![]() , учитывающего распределение
нагрузки по ширине венца, равно:
, учитывающего распределение
нагрузки по ширине венца, равно:
![]() ,
,
![]()
где
![]() - значение коэффициента
- значение коэффициента ![]() в начальный период времени, т.е. без учета
приработки зубьев;
в начальный период времени, т.е. без учета
приработки зубьев;
KFW– коэффициент, учитывающий приработку зубьев.
Среднее
значение коэффициента ![]() , учитывающего добавочную
динамическую нагрузку, можно определять по ГОСТ 21354-75.
, учитывающего добавочную
динамическую нагрузку, можно определять по ГОСТ 21354-75.
Среднее
значение коэффициента ![]() , учитывающего распределение
нагрузки между зубьями
, учитывающего распределение
нагрузки между зубьями
- для косозубых передач:
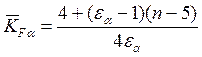 ,
,
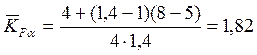
где n – степень точности передачи.
Если
значения ![]() получаются больше единицы, то принимают
получаются больше единицы, то принимают ![]() =1, что соответствует приложению нагрузки в
вершине зуба.
=1, что соответствует приложению нагрузки в
вершине зуба.
В
качестве предельной величины расчетного параметра принимают предел выносливости
зубчатого колеса при изгибе sF
lim
. Среднее значение предела выносливости ![]() :
:
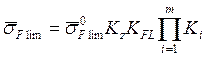 ,
,
![]()
где
![]() - среднее значение предела выносливости
зубьев базового образца – зубчатого колеса модулем 3 мм;
- среднее значение предела выносливости
зубьев базового образца – зубчатого колеса модулем 3 мм;
Kz– коэффициент, учитывающий многоэлементность (многозубость) зубчатого колеса;
KFL – коэффициент долговечности;
ÕKi – произведение корректирующих коэффициентов, учитывающих отличие коэффициентов концентрации и шероховатостей поверхностей выкружек базового и рассчитываемого колеса, масштабный фактор, технологию изготовления, назначаемых на основе накопленных ранее результатов исследований.
В обычных расчетах предел выносливости задают для типовых материалов и способов упрочнения в функции твердости или в виде числовых значений:
-
для нормализованных или улучшенных сталей - ![]() = 1,35
НВ + 100,
= 1,35
НВ + 100,
![]() = 1,35 *300 + 100 = 505
= 1,35 *300 + 100 = 505
где НВ – твердость по Бринеллю;
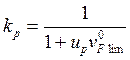 ,
,
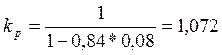
где ![]() - коэффициент вариации предела
выносливости зубьев базового образца:
- коэффициент вариации предела
выносливости зубьев базового образца:
- для нормализованных и
улучшенных зубчатых колес - ![]() =0,08…0,1;
=0,08…0,1;
- для зубчатых колес с
объемной закалкой ТВЧ - ![]() = 0,1…0,14;
= 0,1…0,14;
- для азотированных
колес - ![]() = 0,1…0,12.
= 0,1…0,12.
Зубчатое
колесо можно рассматривать как последовательную систему, состоящею из z
элементов – зубьев. Разрушение колеса (системы) отождествляем с разрушением
наименее прочного зуба – «слабого звена». Среднее значение и коэффициент
вариации предела выносливости наименее прочного зуба меньше, чем аналогичные
характеристики предела выносливости зубьев. Это учитывается введением в
расчетные зависимости коэффициентов: Кz
и az,
значения которых определены в зависимости от различных значений ![]() , для z
= 20…100 (меньшие значения коэффициентов соответствуют большим числам зубьев):
, для z
= 20…100 (меньшие значения коэффициентов соответствуют большим числам зубьев):
|
|
0,08 |
0,10 |
0,12 |
0,14 |
|
Кz |
0,85…0,80 |
0,80…0,75 |
0,77…0,70 |
0,75…0,65 |
|
az |
0,62…0,54 |
0,65…0,57 |
0,68…0,60 |
0,70…0,66 |
Среднее
значение предела выносливости зубьев ![]() само является случайной
величиной вследствие колебаний твердости, радиуса выкрежки, межплавочного
рассеяния. Поэтому коэффициент вариации
само является случайной
величиной вследствие колебаний твердости, радиуса выкрежки, межплавочного
рассеяния. Поэтому коэффициент вариации ![]() предела
выносливости зубчатого колеса больше коэффициента вариации предела выносливости
базового образца, что учитывается вторым слагаемым:
предела
выносливости зубчатого колеса больше коэффициента вариации предела выносливости
базового образца, что учитывается вторым слагаемым:
![]() ,
,
![]()
где az –параметр, учитывающий многоэлементности зубчатого колеса.
В
статическом аспекте рассеяние предела выносливости зубчатого колеса,
оцениваемое коэффициентом вариации ![]() , складывается из
рассеяния пределов выносливости внутри зубчатого колеса (первое слагаемое) и
между зубчатыми колесами генеральной совокупности (второе слагаемое). На
величину
, складывается из
рассеяния пределов выносливости внутри зубчатого колеса (первое слагаемое) и
между зубчатыми колесами генеральной совокупности (второе слагаемое). На
величину ![]() влияет также величина относительного
градиента напряжений. Чем меньше относительный градиент напряжений, тем больше
коэффициент вариации предела выносливости. Базовое колесо обладает меньшими по
сравнению с рассчитываемым колесам размерами и, следовательно, большими
значениями относительного градиента. Поэтому неучет влияния относительного
градиента напряжений на величину
влияет также величина относительного
градиента напряжений. Чем меньше относительный градиент напряжений, тем больше
коэффициент вариации предела выносливости. Базовое колесо обладает меньшими по
сравнению с рассчитываемым колесам размерами и, следовательно, большими
значениями относительного градиента. Поэтому неучет влияния относительного
градиента напряжений на величину ![]() идет в запас прочности.
идет в запас прочности.
Вероятность
безотказной работы по критерию сопротивления усталости при изгибе PF
определяем по таблице 2 в зависимости от квантили: 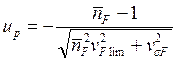 ,
,
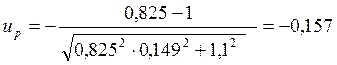
где
![]() - коэффициент запаса прочности по средним
напряжениям, равный:
- коэффициент запаса прочности по средним
напряжениям, равный:
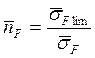
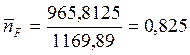
указанную вероятность при необходимости определяются отдельно для колеса и для шестерни. В дальнейших расчетах принимают наименьшее значение.
Искомая вероятность будет равна 0,56.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.