Расчет вероятности безотказной работы зубчатой передачи, страница 2

j - коэффициент, учитывающий приработку и специфику влияния динамической нагрузки на выносливость;

D_а – разность шагов зацепления.

          Коэффициент вариации величины К_HV определяется по формуле:

.

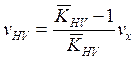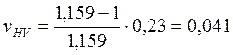
Коэффициент вариации случайной величины Х равен:

,

где v_j - коэффициент вариации величины j;

v_Da – коэффициент вариации величины D_а.

При твердости поверхности зубьев НВ > НВ 350 рекомендуется

j = 0,5…0,75; v_j = 0,114; v_Da = 0,252; при НВ £ НВ 350 - j = 0,25…0,5; v_j = 0,19; v_Da = 0,259.

Для зубьев с твердостью НВ £ НВ 350 динамическую надбавку v_HV следует увеличивать на 30%. Это объясняется тем, что в ГОСТе динамическая надбавка вычисляется при малых значениях коэффициента j; это не полностью компенсируется завышенной разностью D_а, которая больше средней величины D_а в 1,41 раза. Для зубьев с твердостью НВ > НВ 350 ошибки взаимно компенсируются и поправку вводить не следует.

Коэффициент К_Нa, учитывающий участие в передаче нагрузки второй пары зубьев для прямозубых и косозубых колес определяется зависимостью:

K_Ha= a_Ha + b_HaD_a,

K_Ha = a_Ha + b_HaD_a =0,45+1*0,5=0,95

где a_Ha - предельная величина, зависящая от коэффициента перекрытия;

b_Ha - коэффициент пропорциональности, зависящий от передаваемой удельной нагрузки, жесткости, приработки зубьев.

Коэффициент вариации величины К_Нa равен:

,

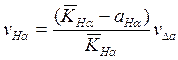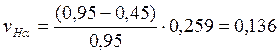
Если значения К_Нa, определенные по рекомендуемой зависимости, получаются больше единицы, то принимают К_Нa = 1.

В качестве предельной величины расчетного параметра принимают предел контактной выносливости зубчатых колес s_{H lim}. Среднее значение напряжения определяется по зависимости:

,

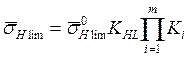где - среднее значение длительного предела выносливости базового образца;

K_HL – коэффициент долговечности;

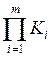- произведение m коэффициентов, учитывающих влияние смазки, размеров зубчатого колеса, шероховатости сопряженных поверхностей зубьев, окружную скорость и т.д. В данном расчете принимаем 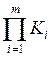=1.

Среднее значение длительного предела выносливости определяется по эмпирическим зависимостям:

  = k_p (aHB + b),

       = 1,092* (2*300 + 70)=731,441

где а и b– постоянные, значения которых выбирают по рекомендациям; для нормализованных и улучшенных сталей а = 2; b = 70;

k_p – коэффициент, учитывающий, какой вероятности неразрушения соответствует определяемый предел выносливости от твердости:

,

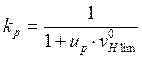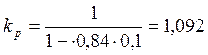
где u_p – квантиль нормированного нормального распределения, зависящая от вероятности неразрушения определяемого предела выносливости;

       - коэффициент вариации длительного предела выносливости базового образца.

В основе рекомендаций по определению предела выносливости заложены результаты усталостных испытаний: вероятность неразрушения приближенно оценивают равной 0,8…0,9, что соответствует квантили u_p = - (0.84…1,28). В зарубежных методиках вероятность неразрушения принимают равной 0,9 или 0,99, что соответствует значению квантили      (–1,28) или (–2,32).

Значение коэффициента вариации длительного предела выносливости образца = 0,08…0,10 – для зубьев без термической обработки их поверхности; = 0,10…0,12 – для поверхностно упрочненных зубьев.

Коэффициент вариации предела выносливости принимают несколько больше, чем для базового образца:

.

Вероятность безотказной работы по критерию сопротивления контактной усталости Р_Н определяется по таблице 2 в зависимости от величины квантили:

,

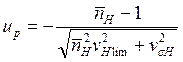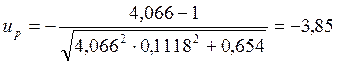
где  - коэффициент запаса прочности по средним напряжениям, равный:

,

.

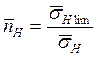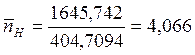Искомая вероятность будет равна 1.

2.2. Расчет на сопротивление усталости при изгибе.

В качестве расчетного параметра принимают напряжение на переходной поверхности зуба s_F, МПа, определяемое по формуле:

,

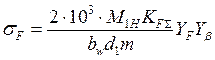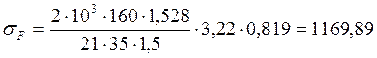
где М_1Н – номинальный крутящий момент на шестерне, Н×м;

b_w– ширина венца, мм;

d₁ – делительный диаметр шестерни, мм;

m – модуль в нормальном сечении зуба, мм;

Y_F – коэффициент, учитывающий форму зуба;

Y_b - коэффициент, учитывающий наклона зуба;

K_FS - коэффициент нагрузки.

Напряжение изгиба s_F рассматривают как случайную величину, которая является функцией от другой случайной величины – коэффициента нагрузки K_FS. Остальные параметры в формуле рассматриваются как детерминированные, способ определения которых можно найти в ГОСТ 21354-75.

Коэффициент нагрузки как при расчете на сопротивление контактной усталости K_HS, так и в донном расчете учитываем одни и те же физические явления. Поэтому структура коэффициента нагрузки аналогичная:

K_FS = K_AK_FbK_FVK_Fa.

K_FS = 1,375*1,09*1,02*1=1,528.

Наименование коэффициентов остаются прежними. Наличие буквы F в индексации коэффициента указывает на его принадлежность к расчетам на изгиб.