Определение характеристик триботехнического качества поверхности. Определение основных характеристик гидростатических подшипников. Составление трибологических моделей механических систем, страница 2

Субмикрошероховатость – более мелкие отклонения, имеющиеся на поверхности микронеровностей. Она обусловлена внутренними дефектами материала, неравномерностью деформирования отдельных кристаллов и т.д. Размеры субмикрошероховатости меньше размеров микронеровностей на два-три порядка. Существенное влияние на формирование субмикрошероховатости оказывает окружающая среда, вызывающая появление пленок различной толщины и состава.

На примере схемы контактирования двух твердых тел с номинальными размерами поверхности контакта B´L, представленной на рис. 1.2, рассмотрим механизм влияния геометрических характеристик на триботехнические процессы.

Номинальная площадь контакта А_а – совпадает с площадью номинальных поверхностей. В данном случае А_а=B´L.

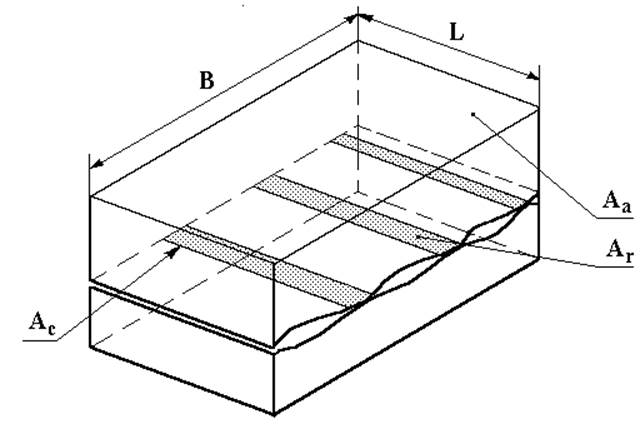
Рис. 1.2. Схема контактирования двух твердых тел с номинально плоскими поверхностями

При контактировании деталей вследствие волнистости их поверхностей фактические пятна контакта будут возникать преимущественно на вершинах волн. Каждая такая область, будучи ограничена контуром, в пределах которого существуют фактические пятна контакта, представляет собой элементарную площадку А_ci. Сумма элементарных площадок образует контурную площадь контакта. Величина ее составляет 5-15% от номинальной площади.

Фактическая площадь контакта А_r – это площадь, на которой осуществляется контакт микронеровностей, образующих шероховатость поверхности. Она обычно мала и составляет 0,01-0,1% от номинальной площади.

Отношения нормальной нагрузки к величинам номинальной        , контурной и фактической площадей дают величины номинального, контурного и фактического давления соответственно:

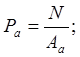
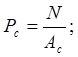
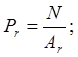                                             (1.1)

Для того, чтобы получить возможность аналитического определения этих величин в зависимости от нагрузки и шероховатости, реальный профиль поверхности заменяют эквивалентной ему моделью. В настоящее время наиболее часто используют сферические модели (набор сфер одинакового радиуса, расположенных на разной высоте от абсолютно жесткого основания (рис. 1.3)). Модель считается адекватной реальному профилю, если соблюдены следующие условия: совпадают механические характеристики; радиус сфер принят равным радиусу кривизны вершин неровностей; опорные площади модели и натуры равны между собой. Опорная площадь является основной характеристикой микрогеометрии поверхности. Ее можно оценивать опорной длиной профиля h, равной сумме длин отрезков b_i, отсекаемых на заданном уровне p_i в материале профиля линией, эквидистантной средней линии в пределах базовой длины l.

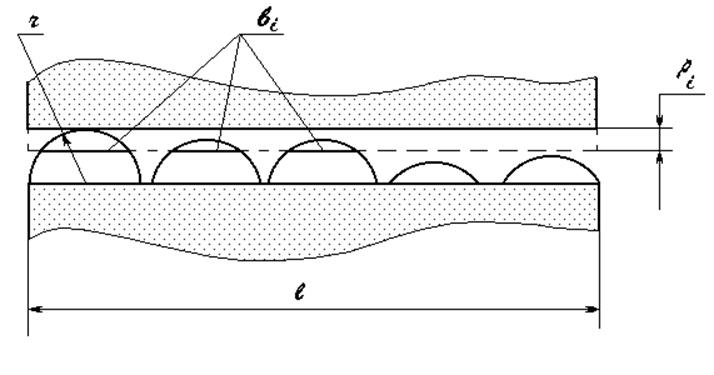
Рис. 1.3. Сферическая модель шероховатости поверхности

В расчетах чаще используют относительную опорную длину профиля t_p, равную отношению опорной длин профиля к базовой длине на заданном уровне сечения p. (t_p=h_p/ l) (рис. 1.4).

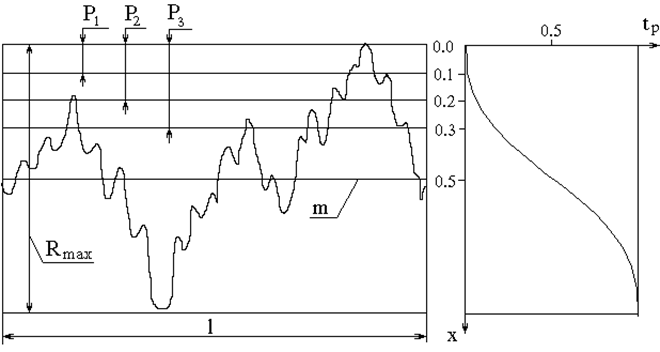
Рис. 1.4. Участок профилограммы и опорная кривая поверхности

Для описания зависимости относительной опорной длины от уровня сечения введен специальный термин "опорная кривая профиля". Из рис. 1.4 видно, что кривая опорной поверхности характеризует распределение материала по высоте шероховатого слоя. Она выражает зависимость относительной опорной длины профиля t_p от относительного сближения сечений x=p/R_max. Для практических инженерных расчетов используется начальный участок (x<0,5) кривой опорной поверхности, расположенный выше средней линии m. Кривая опорной поверхности на этом участке достаточно точно описывается уравнением [1, с.105]

t_p = b ´ x^v                                                 (1.2)

где b, v – параметры степенной аппроксимации.

2. МЕТОДИКА ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК МИКРОГЕОМЕТРИИ

Для определения характеристик микрогеометрии выбирают несколько участков (не менее 5), наиболее характерных для исследуемой поверхности, с которых снимают профилограммы (рис 2.1)

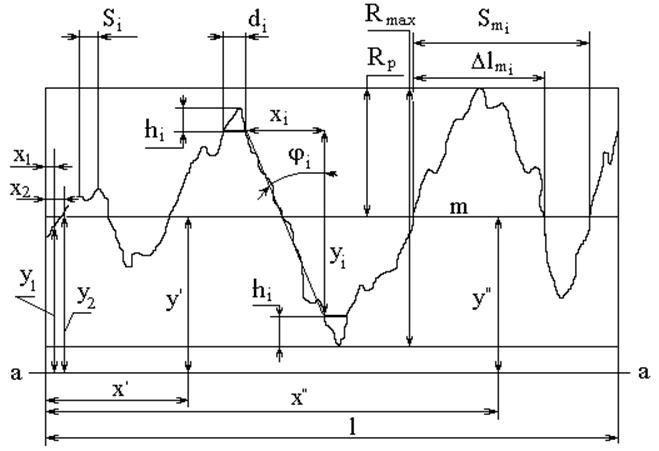
Рис.2.1. Схема обработки профилограммы

Длина профиля участка должна быть не меньше базовой длины.

Среднее арифметическое отклонение профиля R_a отсчитывают непосредственно по шкале профилографа-профилометра.

На профилограммах находят положение средней линии m. Для этого от горизонтальной линии, проведенной параллельно профилю ниже самой глубокой впадины профиля, замеряют ординаты профиля у₁; у₂;-;у_2n через каждые 2 мм. Все полученные значения разбивают на две равные половины для левой и правой частей профилограммы (у₁;-;у_n и у_n;-;у_2n). Среднюю линию проводят через две точки с координатами х¢, у¢ и х¢¢,у¢¢: