Проектирование металлического путепровода: Пояснительная записка к курсовому проекту, страница 2

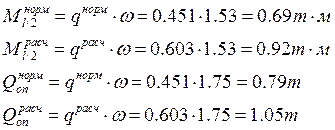
Изгибающий момент в середине пролета продольного ребра принимаем:

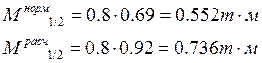
Опорный момент:

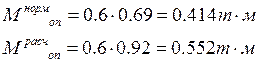
Поперечная сила на 1 ребро в опорном сечении:

Поперечная сила на 1 ребро в середине пролета:

Сведем все полученные усилия в таблицу:

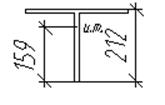
Геометрические характеристики сечения продольного ребра:

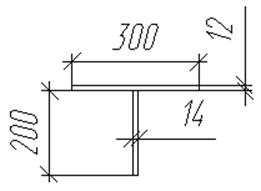
A=0.006431м²

Аст=0.002832 м²

Jx= 0.000027293166 м⁴

Jy= 0.000027047315 м⁴

Значения площади и моментов инерции найдены в программе AutoCAD.

Проверка прочности продольного ребра:

-Нормальные напряжения в середине пролета ребра:

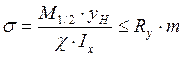
где  - коэффициент, учитывающий ограниченное развитие пластических деформаций в сечении, определяемый из условия

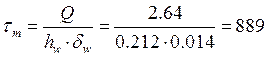 т/м²

h_w – высота сечения, h_w=0,212 м

δ_w – толщина стенки ребра, δ_w=0,014 м

– расчетное сопротивление на сдвиг (принято для стали 15ХСНД)

т/м²

 т/м²

Т.е. условие выполняется 889 < 4356.25

Тогда, , где - коэффициент для тавровых сечений, определяемый по табл.61;

 - коэффициент условий работы

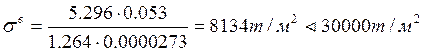
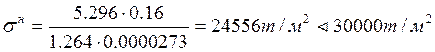
Прочность обеспечена.

-Касательные напряжения в опорном сечении ребра:

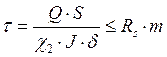, где где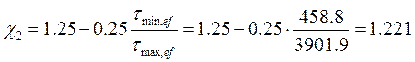 

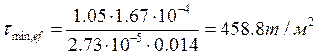
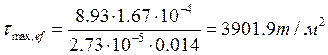
S-статический момент отсеченной части сечения

J-момент инерции

-толщина стенки

– расчетное сопротивление на сдвиг (принято для стали 15ХСНД)

т/м²

m=1 -коэффициент условий работы

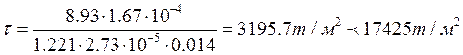
Прочность обеспечена.

Проверка продольного ребра на выносливость.

Согласно примечанию 2 п.2.1 и примечанию 2 п.2.12 СНиП 2.05.03-84* нагрузкой для расчета на выносливость является нагрузка А-11 без учета действия пешеходной нагрузки.

Согласно п.2.3 таблица 6,  расчетные усилия от подвижной нагрузки берутся с коэффициентами:  γ_f =1.0 и 1+2/3μ

(1+μ)=1.37 → (1+2/3μ) = 1.25

Максимальные усилия

= ≤  

≤

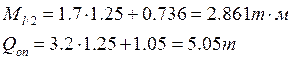
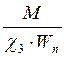– абсолютное наибольшее нормальное напряжение

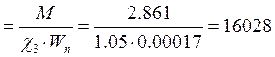 т/м²

 - коэффициент, принимаемый равным 1.05

W_n = I_x/y_n = 0.0000273/0.16=0.00017 м³

– абсолютное наибольшее скалывающее напряжение

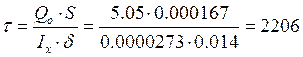 т/м²

По таблице 60 для элементов автодорожных и городских мостов m=1.0.

Коэффициент  определяется по формуле:

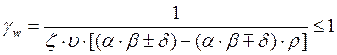, где  ζ=0.7 (для автодорожных мостов)

 коэффициенты, учитывающие марку стали и нестационарность режима нагруженности (табл. 78), для стали 15ХСНД    α=0.72,  δ=0.24

β - эффективный коэффициент концентрации напряжений, принимаемый по табл.1 по обязательному приложению 17.

β = 2.0

 - коэфф., зависящий от длины загружения λ линии влияния при определении

 = v-ξ·λ = 2.09-0.0495·3.5 = 1.92

по таблице 79  v=2.09,  ξ=0.0495              

λ=3.5 м – длина ребра

ρ- коэффициент ассиметрии цикла переменных напряжений

ρ=min M_1/2/max M_1/2=0.736/2,861=0.257

ρ=min Q_оп/max Q_оп=1.05/5.05=0.208

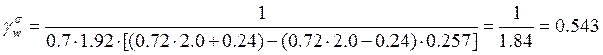
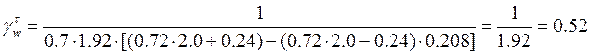
Проверка на выносливость

                                                               ≤

16028< 0.543·30000·1.0                                                       2206 < 0.75·0.52·30000·1

16028 < 16290                                                                      2206 < 11700

Выносливость обеспечена.

2.2. Расчет поперечного ребра.

Усилия в поперечой балке:

Давление на ребро от нагрузки одного ряда колес нагрузки А-11:

Давление от полосовой составляющей нагрузки А-11:

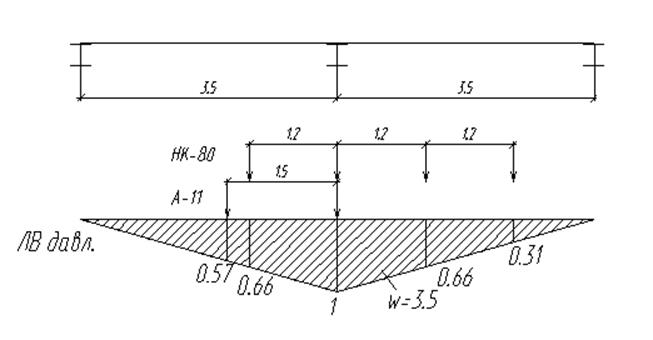
Давление от ряда колес нагрузки НК-80:

От пешеходной нагрузки:

p = 400-2·λ = 400 - 2·7 = 386 кг/м²=0.386 т/м²

где λ = 6 м – длина загружения

Линии влияния усилий (построены в «Лире»).

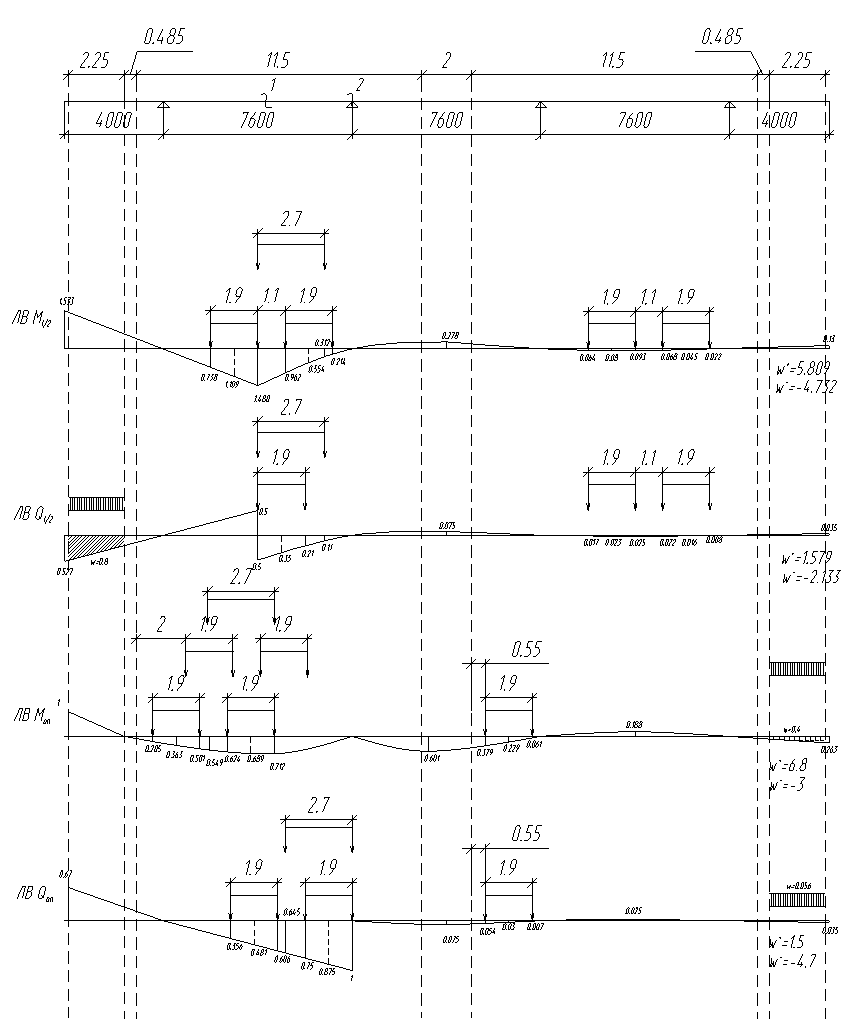
1)  Нагрузка А-11

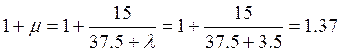
λ=3.5м – длина участка загружения

γ_f^{равн. распр.} =1.2,  γ_f^тел.=1.5

Коэффициент полосности для нагрузки А-11: тележка S₁ = 1.0 - всегда,

для распределенной нагрузки S₂ = 1.0 - 1 полоса, S₂ = 0.6 – 2 и последующие полосы.

М^норм. =

М^расч =

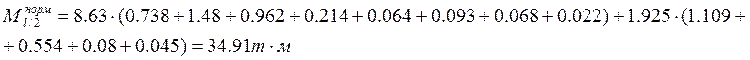
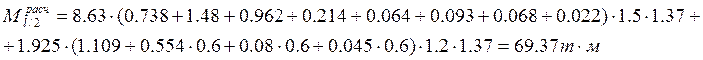
У барьерного ограждения

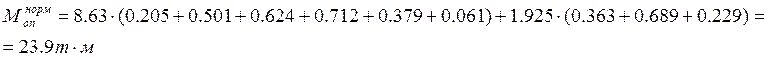
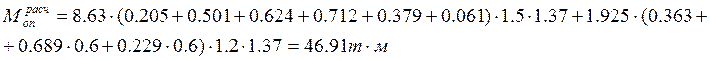
У полосы безопасности

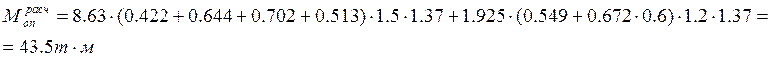
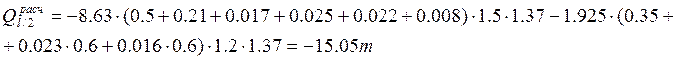
У полосы безопасности

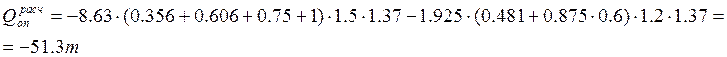
У барьерного ограждения

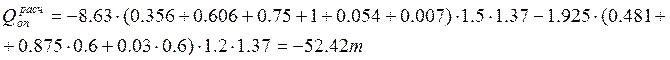
2)  Нагрузка НК-80