









ВОПРОСЫ К ЭКЗАМЕНУ ЗА ПЕРЫВЙ СЕМЕСТР.
Основная
задача кинематики состоит в определении положения и состояния объекта быстроту
перемещения вектора средней скорости 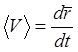 ;
; ![]() =>
=> 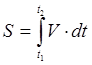 . При
вращательном движении точки лежащая на одном радиусе будут иметь разные
линейные скорости, поэтому линейная скорость не может быть характеристикой
вращательного движения, такой характеристикой является угол поворота.
. При
вращательном движении точки лежащая на одном радиусе будут иметь разные
линейные скорости, поэтому линейная скорость не может быть характеристикой
вращательного движения, такой характеристикой является угол поворота.
Tвр = Izw²/2 – кинетическая энергия
вращающегося тела; T=mv²/2 –
поступательное движения (получено II З-н Ньютона + dA=dT *dr).
При их сравнении следует, что момент инерции – мера инертности тела при
вращательном движении. В случае плоского движения тел например цилиндра,
скатывающегося по наклонной плоскости можно получить как сумма поступательного
движения и энергии вращения. 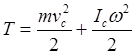
Для
характеристики быстроты изменения угла ![]() вводят
понятие угловой скорости.
вводят
понятие угловой скорости. ![]() - угловая скорость.
- угловая скорость. 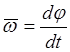 .
. 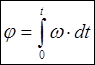 -
формула для расчета угла поворота.
-
формула для расчета угла поворота.
Причиной
механического движения являются различные взаимодействия F
– сила. Сила. Величина векторная. Подчинена принципу суперпозиции. 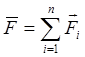 . По направлению результирующая сила
совпадает с ускорением. На быстроту движения тела влияет не только приложенная
сила, но и инертность этого тела. Инертность характеризует свойство тел,
препятствует изменению их скорости. Количественной мерой инертности является
масса, т.е. более инертные тела обладают большей массой. Масса аддитивна
. По направлению результирующая сила
совпадает с ускорением. На быстроту движения тела влияет не только приложенная
сила, но и инертность этого тела. Инертность характеризует свойство тел,
препятствует изменению их скорости. Количественной мерой инертности является
масса, т.е. более инертные тела обладают большей массой. Масса аддитивна 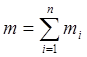 , величина скалярная и при малых скоростях
не изменяется. Не только мера инертности, но и причина гравитации. Импульс
, величина скалярная и при малых скоростях
не изменяется. Не только мера инертности, но и причина гравитации. Импульс ![]() . При вращательном движении большое
значение имеет не только величина приложенной силы, но и точка ее приложения
для учета этого фактора вводится понятие момента силы. Моментом силы
относительно неподвижной точки О называют векторное произведение радиус вектора
проведенного из точки О в точку приложения силы на саму эту силу.
. При вращательном движении большое
значение имеет не только величина приложенной силы, но и точка ее приложения
для учета этого фактора вводится понятие момента силы. Моментом силы
относительно неподвижной точки О называют векторное произведение радиус вектора
проведенного из точки О в точку приложения силы на саму эту силу. ![]() ;
;![]() (
(![]() - плечо силы)
- плечо силы)
I закон Ньютона: всякая материальная точка сохраняет свое состояние покоя или равномерное прямолинейное движение до тех пор, пока воздействие со стороны других тел не заставит изменить ее это состояние. Первый закон Ньютона выполняется не во всех системах отсчета, а те к которым он выполняется называют инерциальными системами отсчета. Инерциальной системой является такая система отсчета, относительно которой материальная точка, свободная от внешних действий, либо покоится. Либо движется равномерно и прямолинейно.
Законы динамики одинаковы во всех инерциальных системах отсчета – принцип относительность Галилея. Для доказательства возьмем две системы отсчета: инерциальную систему K(x,y,z) и K`(x`,y`,z`), k` движется относительно К равномерно и прямолинейно со скоростью U – const. Скорость направлена вдоль OO`, радиус вектор, проведенный из О в О`, r0=ut => r=r`+r0=r`+ut – уравнение преобразования Галилея.
3. Понятие момента силы. Момент силы относительно точки, относительно оси. Момент инерции. Теорема Штейнера.
Моментом силы
относительно неподвижной точки О называют векторное произведение радиус вектора
проведенного из точки О в точку приложения силы на саму эту силу. ![]() ;
;![]() (
(![]() - плечо силы). Момент силы относительно
точки О есть векторная величина, а момент силы относительно оси проходящий
через эту точку есть скалярная величина. Моментом силы относительно неподвижной
оси z называется скалярная величина
- плечо силы). Момент силы относительно
точки О есть векторная величина, а момент силы относительно оси проходящий
через эту точку есть скалярная величина. Моментом силы относительно неподвижной
оси z называется скалярная величина ![]() равная проекции на эту ось вектора М
момента силы, определенного относительно произвольной точки О данной оси z. Значение момента не зависит от выбора положения точки О на
оси z
равная проекции на эту ось вектора М
момента силы, определенного относительно произвольной точки О данной оси z. Значение момента не зависит от выбора положения точки О на
оси z 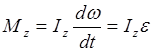 .
Момент инерции. Опыт показывает, что скорость вращения зависит не только от
приложения силы от точки ее приложения, но и от того, как распределена масса
относительно оси вращения этот факт и учитывает понятие момент инерции
.
Момент инерции. Опыт показывает, что скорость вращения зависит не только от
приложения силы от точки ее приложения, но и от того, как распределена масса
относительно оси вращения этот факт и учитывает понятие момент инерции ![]() . Физический смысл момента инерции. Момент
инерции является мерой инертности при вращательном движении (чем больше I тем труднее раскрутить тело). Не всегда тела вращаются
вокруг собственной оси. Если наблюдать вращение тел относительно произвольной
оси, не проходящей через центр, то расчет места инерции принимает теорема
Штейнера
. Физический смысл момента инерции. Момент
инерции является мерой инертности при вращательном движении (чем больше I тем труднее раскрутить тело). Не всегда тела вращаются
вокруг собственной оси. Если наблюдать вращение тел относительно произвольной
оси, не проходящей через центр, то расчет места инерции принимает теорема
Штейнера ![]() .
.
4. Понятие момента импульса. Момент импульса тела относительно точки, относительно оси. Основной закон динамики вращательного движения.
Моментом импульса
материальной точки А относительно неподвижной точки О называется физическая
величина, определяем векторным произведением: ![]() , где r
– радиус вектор из точки О в точку А; p=mv импульс материальной
точки. Модуль вектора момента импульса
, где r
– радиус вектор из точки О в точку А; p=mv импульс материальной
точки. Модуль вектора момента импульса ![]() ;
; ![]() - угол между векторами r
и p. Моментом импульса относительно неподвижной оси z
называется скалярная величина Lz, равная проекции на эту ось вектора момента
импульса, определенного относительно произвольной точки О данной оси. Момент
импульса Lz не зависит от положения точки О на оси z
- угол между векторами r
и p. Моментом импульса относительно неподвижной оси z
называется скалярная величина Lz, равная проекции на эту ось вектора момента
импульса, определенного относительно произвольной точки О данной оси. Момент
импульса Lz не зависит от положения точки О на оси z 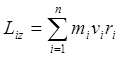 . Момент импульса твердого тела
относительно оси равен произведению момента инерции тела относительно той же
оси на угловую скорость
. Момент импульса твердого тела
относительно оси равен произведению момента инерции тела относительно той же
оси на угловую скорость ![]() .
. 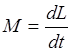 - основной закон динамики вращательного
движения.
- основной закон динамики вращательного
движения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.