Ответы на экзаменационные вопросы № 1-31 по курсу "Физика" (Кинематические характеристики поступательного и вращательного движения. Ток смещения, его отличие и сходство с током проводимости. Закон полного тока), страница 4

15.  Вероятность события, функция распределения (примеры). Закон Гиббса. Функция распределения Гиббса.

Из МКТ следует, что частицы находятся в непрерывном, хаотическом движении, поэтому точно определить в данный момент времени координаты и скорость невозможно, т.е. все микропараметры – это величины случайные.

Случайные величины описывают математический аппарат, который называется теорией вероятности. 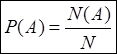; P(A) – частота события она характеризует отношения опыта который производится в данный момент к общему опыту. P(A) > 0 – событие достоверное, P(A) = 0 – событие никогда не произойдет.

w - вероятность. Вероятностью – называется частота при N ® 0 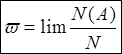; Для совокупности частиц вероятность характеризует долю частиц, для которой доли частиц, находятся на интервале от x до x + dx 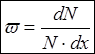 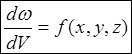- функция распределения. Функция распределения используется для нахождения средних значений случайных величин. 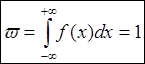  - условие нормировки. 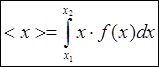, где f(x)dx - dv - характеризует вероятность выпадения этой величины.

16.  Распределение энергии молекул идеального газа по проекции скорости (распределение Гаусса), его анализ.

После того как в сосуд накачивается воздух, первоначальная масса газа будет сжата и если закачивание произведено достаточно быстро, то процесс близок адиабатическому и приводит повышению давления и температуры воздуха в баллоне. Через некоторое время происходит остывание газа вследствие теплопроводности стенок баллона. После открытия крана воздух в сосуде расширяется адиабатически, и давление становится равным атмосферному.

Адиабатическими называют процессы, протекающие без теплообмена с внешней средой. Это возможно при хорошей теплоизоляции либо при кратковременном протекании процесса.

¶Q = 0; Q = 0, , т.е. работа совершается газом, происходит за счет изменения внутренней энергии если: dV > 0 , то dT < 0

dV < 0 , то dT > 0.

как и в 1. 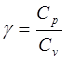; g - коэффициент Пуассона.        

Удельная теплоемкость вещества – величина равная количеству теплоты, необходимая для нагревания 1 кг. Вещества на 1 К. 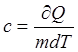[дж/(кг*К)]

Молярная теплоемкость  величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К. 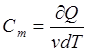; где v=m/M – количество вещества.

17.   Распределение молекул идеального газа по модулю скорости (распределение Максвелла), его анализ.

По молекулярно кинетической теории, как бы не изменялись скорости молекул при столкновениях,  средняя квадратичная скорость молекул массой m₀ в газе, находящемся в состоянии равновесия при T-const, остается постоянной и равной . Закон Максвелла описывается функцией называемой функцией распределения молекул по скоростям. Функция определяет относительное число молекул dN(v)/N, скорости которых лежат на интервале от v до v+dv т.е.  => 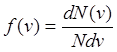. Максвелл нашел функцию f(v) – закон о распределении молекул идеального газа по скоростям: 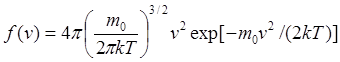 (1). Относительное число молекул dN(v)/N, скорости лежат на интервале от v до v+dv, это значит что функция f(v) удовлетворяет услови. нормировки. 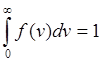. Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью. Его можно получить продеференцировав выражение (1). 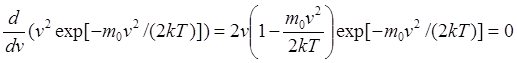 , если v = 0, то получим

18.  Степени свободы. Распределение энергии молекул по степеням свободы. Основное уравнение МКТ для энергии и давления (вывод).

Степень свободы – это число независимых переменных, полность. Определяющих положение системы в пространстве. Для всех многоатомных молекул число степеней свободы равно шести i=i_пост+i_вращ+i_колеб. Для нахождения энергии приходящейся на одну степень свободы достаточно найти среднюю энергию движения молекул вдоль какой-то оси 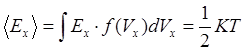.  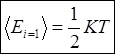- теорема распределения энергии по степеням свободы. Если система находится в равновесии и энергия частиц рассчитывается по формуле E=ax², то на одну степень свободы приходится энергия равная 1/2KT. <E>=i*1/2KT – основное уравнение МКТ для энергии. Определим давление газа в объеме V, температуре T. P=F/S. Для расчета силы с которой 1 моль будет взаимодействовать со стенкой используют II закон Ньютона 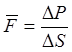=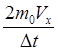. 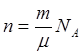; ; 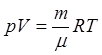 =>  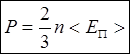- связь между макро и микропараметрами мира, основное уравнение МКТ для давления. Давление смеси газов равно сумме пропорциональных давлений, т.е. давлений созданным каждым газом в отдельности, если бы он один занимал весь предоставленный объем (закон Дальтона) .