Ответы на экзаменационные вопросы № 1-31 по курсу "Физика" (Кинематические характеристики поступательного и вращательного движения. Ток смещения, его отличие и сходство с током проводимости. Закон полного тока), страница 3

10.  Колебания. Гармонические Колебания. Дифференциальное уравнение гармонических  колебаний. Формула периода колебаний пружинного маятника (вывод).

Колебания – самый распространенный вид движения в природе. Колебанием называется любой процесс, который периодически повторяется в зависимости от характера воздействия на колеблющуюся систему различают – свободное колебание, вынужденное, автоколебания, параметрические. Свободные колебания возникают в системе которая предоставлена самой себе, после того как была выведена из состояния равновесия. Самыми простыми колебаниями в механике являются гармонические. Гармонические колебания – это колебания, протекающие по закону синуса или косинуса. Основные признаки: Колеблющаяся система смещается относительно состояния равновесия, колеблющиеся движения обладают периодичностью во времени , количественной характеристикой этого колебания является период. Т – период одного полного колебания (колеб волна). Для начала колебания необходимо наличие внешней силы. Второй закон Ньютона для осциллятора ; - дифференциальное уравнение 2-го порядка для гармонических колебаний, если вторая производная из какого-либо параметра пропорциональна этому параметру, взятому со знаком “-“, то это является признаком гармонического колебания .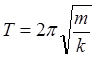

11.  Математический и физический маятники, формулы периода их колебаний (вывод).

Для нахождения колебания необходимо выполнить следующие операции: Определить значение результирующей силы, Подставить это значение во II закон Ньютона и получить дифференциальное уравнение 2-го порядка. Математический маятник – это тело небольшой массы подвешан на тонкой нерастяжимой нити. 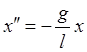;  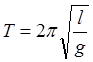- формула периода колебания математического маятника. Физический маятник – это любое совершающее колебание относительно точки подвеса. Закон поступательного движения применить нельзя т.к. точки вращения тела будут иметь разные линейные скорости т.е. разные ускорения. Применим основной закон вращательного движения 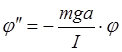; 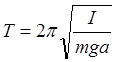- период колебаний физического маятника (I – момент инерции).

12.  Затухающие колебания. Дифференциальное уравнение затухающих колебаний, его решение. Характеристики затухающих колебаний.

Если в системе на колеблющееся тела кроме квазеупругой силы действует сила сопротивления, то колебания будут затухающими. ;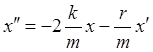=> - дифференциальное ур-е второго порядка для затухающих колебаний. - время релаксации – это время по истечение которого амплитуда уменьшается в е раз. - добротность – характеризует изменение энергии за одно колебание.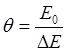

13.  Вынужденные колебания. Дифференциальное уравнение вынужденных колебаний, его решение. Механический резонанс.

Все колебания происходящие в реальных условиях являются затухающими, т.к. всегда действует сила сопротивления, поэтому необходимо постоянно пополнять системы.  =>  =>  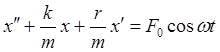=> - дифференциальное ур-е второго порядка для вынужденных колебаний. Зависимость амплитуды от частоты приводит к тому, что на определенной частоте сильно возрастает амплитуда – это явление называется резонансом,  - точное выражение для резонансной частоты. 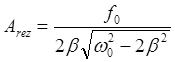 - ф-ла для расчета резонансной амплитуды.

14.  Механические волны. Уравнение плоской волны.  Свойства волн.

Механические волны – это есть процесс распределение колебаний в упругой среде. Если одна молекула выведена из равновесия, то при обратном движении она передает импульс окружающим молекулам, те в свою очередь другим, так образуется механическая волна. Волновая поверхность – это геометрическое место точек совершающее колебание в одинаковой фазе (плоскость). Получим уравнение плоской волны, т.е. волны распространяющейся в одном направлении. 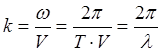(к – волновое число, показывает ск-ко длин волн на раст 2p)  - длина волны.  - уравнение плоской бегущей волны. Свойства: любая бегущая волна переносит e в направлении ее распространения, волны характеризуются периодичностью во времени и пространстве, различает фазовую скорость волн в упругой среде.