Ответы на экзаменационные вопросы № 1-31 по курсу "Физика" (Кинематические характеристики поступательного и вращательного движения. Ток смещения, его отличие и сходство с током проводимости. Закон полного тока), страница 5

19.  Первое начало термодинамики, его применение к изопроцессам.

Термодинамика рассматривает процессы протекающие в системах в целом т.е. не рассматривает из чего состоит эта система. V – const – изохорный 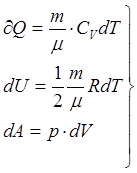A=0, т.к. dV=0 .  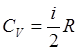- молярная теплоемкость при постоянном объеме. P –const – изобарный 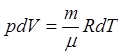;  - уравнение Майера. С_p > C_v т.к. при изобарном процессе подведенная теплота расходуется не только на изменение внутренней энергии, но и на совершение работы R – характеризует работу которую нужно совершить чтобы 1 моль вещества потратить на 1º. Т – const – изотермический процесс .  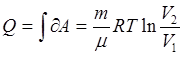- формула работы (теплоты) при изотермических процессах. Адиабатный процесс – это процесс, протекающий без теплообмена с окружающей средой , т.е. работа, совершаемая газом происходит за счет изменения внутренней энергии. Два способа получения адиабатного процесса работа имеет хорошую теплоизоляцию, малая скорость протекания реакций. Для каждого изопроцесса существует уравнение, объединяющее их макропараметры, такое уравнение существует для адиабатного процесса   - уравнение Пуассона. ;  При адиабатическом процессе давление зависит не только от концентрации газа, но и от температуры.

20.  Удельная и молярная теплоемкость. Вывод уравнения Майера.

Удельная теплоемкость вещества – величина, равная количеству теплоты, необходимому для нагревания 1 кг веществ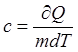а на 1 К:  (с – единица удельной теплоемкости – (Дж/(кг*К)). Молярная теплоемкость – величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К: 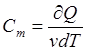, единица молярной теплоемкости (Дж/(Моль*К)), где v=m/M – количество вещества. , где М – молярная масса вещества. Запишем выражение первого начала термодинамики для 1 моль газа , если газ нагревается при постоянном объеме, то работа внешних сил равна нулю и сообщаемая газу из вне теплота идет на увеличение его внутренней энергии 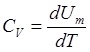, т.е. молярная теплоемкость газа при постоянном объеме C_V равна изменению внутренней энергии 1 моль газа, тогда  => 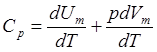, поскольку dT не зависит от вида процесса получим  - уравнение Майера; оно показывает, что C_p всегда больше С_V на величину молярной газовой постоянной. Это объясняется тем, что при нагревании газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа.

21.  Обратимые и необратимые процессы. Статистический вес. Статистическое и термодинамическое определение энтропии. Связанная и свободная энергия.

22.  Второе начало термодинамики. Цикл Карно, КПД тепловых машин.

23.  Локальные и интегральные характеристики электрического и магнитного полей.

24.  Записать систему уравнений Максвелла, дать формулировку каждого уравнения и его физический смысл.

25.  Теорема Остроградского-Гаусса, ее применение для расчета напряженности поля, созданного заряженной нитью.

Поток вектора напряженности через замкнутую поверхность S, равен алгебраической сумме зарядов находящихся внутри этой поверхности деленной на ee₀ 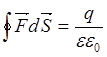 - Тh. Остроградского-Гаусса. 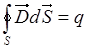, где D – вектор индукции. Теорема Остроградского-Гаусса применяется только для расчетов симметричных электростатических полей (сферическая, зеркальная, осевая). (рис) ; ; 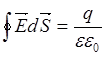==E*2Пvl => .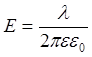

26.  Получите формулу для расчета работы электростатического поля по переносу заряда, проанализируйте ее.