Ответы на экзаменационные вопросы № 1-31 по курсу "Физика" (Кинематические характеристики поступательного и вращательного движения. Ток смещения, его отличие и сходство с током проводимости. Закон полного тока), страница 2

5.  Законы динамики в неинерциальных системах отсчета.

Системы отсчета,  движущиеся относительно инерциальной системы с ускорением, называют неинерциальными. В неинерциальных системах законы Ньютона несправедливы, но здесь действительны силы особого рода, так называемые силы инерции. Если учесть силы инерции, то второй закон ньютона будет справедлив для любой системы отсчета: произведение массы тела на ускорение в рассматриваемой системе равно сумме всех сил, действующих на данное тело. Силы инерции F_ин при этом должны быть такими, чтобы вместе силами F, обусловленными воздействием тел друг на друга, они сообщали телу ускорение а, каким оно обладает в неинерциальных системах отсчета  => .

6.  Механическая работа. Работа переменной силы. Понятие консервативных и не консервативных сил. Примеры расчетов работы. Мощность.

Консервативные силы – это силы работы, которые не зависят от формы траектории движения, а определяются только начальной положения тел (mg, F_упр). Неконсервативные силы зависят от формы траекторий(F_тр, F_сопр, F_g, F_т). Из определения следует, что работа силы упругости – это консервативная сила упругости. Мощность N. Характеризует работу выполняемую в единице времени. ;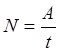

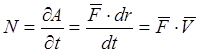
7.  Потенциальная энергия и ее свойства. Кинетическая энергия и ее свойства. Полная механическая энергия.

Е_п  > < 0, т.к. ее значение зависит от выбора нулевого уровня, а физический смысл имеет не сама энергия, а ее изменение. Е_п – это однозначная непрерывная функция состояния. Непрерывная в классической механике энергия объекта может меняться на любую сколь угодно малую величину, говорят, энергия имеет сплошной спектр, т.е. она не квантуется. Функция состояния означает, что энергия не зависит от того, как тело пришло в это состояние. Если работа консервативных сил совершается в замкнутой системе, то все процессы идут в сторону убывания потенциальной энергии . Все движения тела обладают кинетической энергией.;  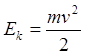Свойства: Однозначная непрерывная функция состояния, , Е_к – величина аддитивная, изменить кинетическую энергию могут внешние и внетренние силы (консервативн. и не консервативн).

8.  Законы сохранения в механике. Закон сохранения механической энергии (вывод).

Закон сохранения энергии – результат обобщения многих экспериментальных данных. Идея этого закона принадлежит Ломоносову, а формулировка закона сохранения энергии дана немецким врачом Майером. Различают три вида фундаментальной симметрии параллельный перенос осей координат – она обусловлена однородностью пространства, симметрия относительно поворота осей координат – обусловлена изотропностью, симметрия относительно выбора начала координат – обусловлена однородностью времени. Рассмотрим систему материальных точек массами m₁,…,m_n, движущиеся со скоростями v₁,…,v_n. Пусть  - равнодействующие внутренних консервативных сил, действующие на каждую из этих точек, а F₁,…,F_n – равнодействующая внешних сил. При  массы материальных точек постоянны и уравнения второго закона ньютона следующие.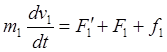 ((f-равнодействующая)… n). Двигаясь под действием сил, точки за время dt совершают перемещения равные dr₁,…,dr_n. Умножив каждое уравнение скалярно, получим (…n).Сложив их получим 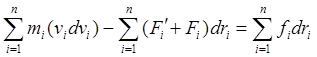® d(T+П)=dA ® T+П=E=const – закон сохранения механической энергии.

9.  Формулировка и вывод закона сохранения импульса и момента импульса.

Система считается замкнутой, если на нее не действуют внешние силы или их результирующая равна нулю или ими можно пренебречь. Пусть система состоит из N объектов 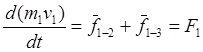(-/8/-). 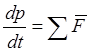_внеш – закон сохранения импульса т.е. импульс системы могут изменить только внешние силы, а если система замкнута 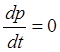 => . Суммарный импульс системы есть величина постоянная, если система замкнута. Если внешние силы действуют, но их проекция равна нулю, то систему в этом направлении можно считать замкнутой и можно применить закон сохранения импульса. // Пусть дана система частиц, положение которой относительно т. О определяется соответственно радиус векторами. Запишем для каждой материальной точки второй закон ньютона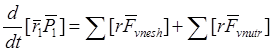(-/8/-). По третьему закону Ньютона тела взаимодействуют с одинаковыми по модулю силами, поэтому плечо силы одинаковое и F_внутр = 0 => 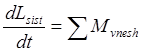- закон изменения момента импульса, производная от момента импульса системы по времени равна суммарному моменту внешних сил, т.е. измекнить момент импульса могут только внешние силы, а внешние силы не действуют или их результирующий момент равен нулю, получим 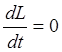=> L=const.