Министерство образования и науки
Новокузнецкий институт (филиал)
федерального государственного бюджетного
общеобразовательного учреждения
Высшего профессионального образования
«Кемеровский государственный университет»
Кафедра экономики
ПРАКТИЧЕСКАЯ РАБОТА
по дисциплине «УПРАВЛЕНИЕ КАЧЕСТВОМ»
по теме: «Статистическое управление процессами. Контрольные карты»
Выполнили:
Студенты группы МО-09
Фаррахова М.
Тюканова С
Проверил:
профессор, д.т.н.
М. В. Попова
Новокузнецк 2013
1. Менеджер по качеству компании-импортера чая предъявляет следующие требования к процессу упаковки, известные ему из аналогичных упаковочных процессов:
• Средний вес упаковки 100,6 г.,
• Стандартное отклонение 1,4 г.
Для контроля были взяты 25 выборок объемом 5 пачек. Значения их средних и размахов приведены в таблице 7.
|
№ п/п |
Среднее подгруппы |
Размах подгруппы |
№ п/п |
Среднее подгруппы |
Размах подгруппы |
|
1 |
100,6 |
3,4 |
14 |
99,4 |
5,1 |
|
2 |
101,3 |
4,0 |
15 |
99,4 |
4,5 |
|
3 |
99,6 |
2,2 |
16 |
99,6 |
4,1 |
|
4 |
100,5 |
4,5 |
17 |
99,3 |
4,7 |
|
5 |
99,9 |
4,8 |
18 |
99,9 |
5,0 |
|
6 |
99,5 |
3,8 |
19 |
100,5 |
3,9 |
|
7 |
100,4 |
4,1 |
20 |
99,5 |
4,7 |
|
8 |
100,5 |
1,7 |
21 |
100,1 |
4,6 |
|
9 |
101,1 |
2,2 |
22 |
100,4 |
4,4 |
|
10 |
100,3 |
4,6 |
23 |
101,1 |
4,9 |
|
11 |
100,1 |
5,0 |
24 |
99,9 |
4,7 |
|
12 |
99,6 |
6,1 |
25 |
99,7 |
3,4 |
|
13 |
99,2 |
3,5 |
Построить ![]() и R – карты и оценить
статистическую управляемость процесса упаковки чая.
и R – карты и оценить
статистическую управляемость процесса упаковки чая.
Х карта.
CL = ![]() = 100,056
= 100,056
![]() = 4,156
= 4,156
UCL=![]() +А2
+А2![]() = 100,056 + 0,577*4,156=102,5
= 100,056 + 0,577*4,156=102,5
LCL= ![]() –А2
–А2![]() =100,056-0,577*4,156=97,6
=100,056-0,577*4,156=97,6
R карта
CL=![]() =4.156
=4.156
UCL=D4![]() =2.114*4.156=8,78
=2.114*4.156=8,78
LCL=D3![]() =0*4.156=0 – не определен
=0*4.156=0 – не определен
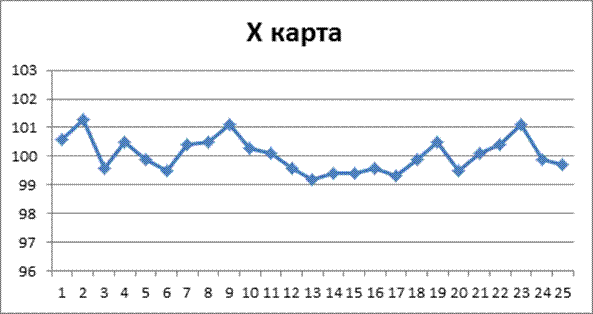
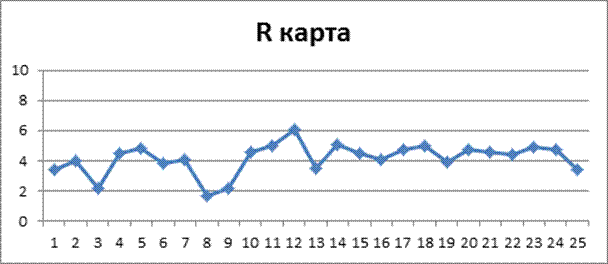
Вывод: Процесс статистически управляемый.
2. Наладчик произвел настройку автоматического станка на номинальный размер 35 и стандартное отклонение 4,2.
Для проверки правильности настройки станка проведен контроль колебаний качества изделий от партии к партии. Для этого из каждой партии бралась малая выборка объемом 5 деталей. В таблице 8 показаны результаты обработки данных десяти выборок.
|
№ выборки |
Среднее арифметическое |
Размах |
|
1 |
36,0 |
6,6 |
|
2 |
31,4 |
0,5 |
|
3 |
39,0 |
15,1 |
|
4 |
35,6 |
8,8 |
|
5 |
38,8 |
2,2 |
|
6 |
41,6 |
3,5 |
|
7 |
36,2 |
9,6 |
|
8 |
38,0 |
9,0 |
|
9 |
31,4 |
20,6 |
|
10 |
29,2 |
21,7 |
Оцените возможности статистической управляемости процесса обработки деталей на автоматическом станке.
Х карта.
CL = ![]() = 35,72
= 35,72
![]() = 9,76
= 9,76
UCL=![]() +А2
+А2![]() = 35,72 + 0,577*9,76=41,35
= 35,72 + 0,577*9,76=41,35
LCL= ![]() –А2
–А2![]() =35,72-0,577*9,76=30,09
=35,72-0,577*9,76=30,09
R карта
CL=![]() =9,76
=9,76
UCL=D4![]() =2.114*9,76=20,63
=2.114*9,76=20,63
LCL=D3![]() =0*9.76=0 – не определен
=0*9.76=0 – не определен
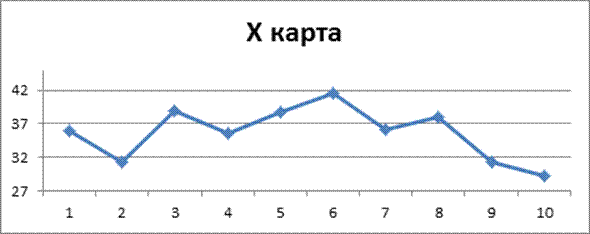
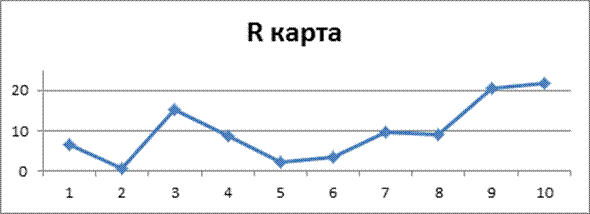
Вывод: процесс статистически не управляемый.
3. В таблице 9 приведены результаты измерений внешнего радиуса втулки. Каждые полчаса делались четыре измерения. Всего взято 20 выборок.
|
№ подгруппы |
Радиус |
|||
|
Х1 |
Х2 |
Х3 |
Х4 |
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
0,1898 |
0,1729 |
0,2067 |
0,1898 |
|
2 |
0,2012 |
0,1913 |
0,1878 |
0,1921 |
|
3 |
0,2217 |
0,2192 |
0,2078 |
0,1980 |
|
4 |
0,1832 |
0,1812 |
0,1963 |
0,1800 |
|
5 |
0,1692 |
0,2263 |
0,2066 |
0,2091 |
|
6 |
0,1621 |
0,1832 |
0,1914 |
0,1783 |
|
7 |
0,2001 |
0,1937 |
0,2169 |
0,2082 |
|
8 |
0,2401 |
0,1825 |
0,1910 |
0,2264 |
|
9 |
0,1996 |
0,1980 |
0,2076 |
0,2023 |
|
10 |
0,1783 |
0,1715 |
0,1829 |
0,1961 |
|
11 |
0,2166 |
0,1748 |
0,1960 |
0,1923 |
|
12 |
0,1924 |
0,1984 |
0,2377 |
0,2003 |
|
13 |
0,1768 |
0,1986 |
0,2241 |
0,2022 |
|
14 |
0,1923 |
0,1876 |
0,1903 |
0,1986 |
|
15 |
0,1924 |
0,1996 |
0,2120 |
0,2160 |
|
16 |
0,1720 |
0,1940 |
0,2116 |
0,2320 |
|
17 |
0,1824 |
0,1790 |
0,1876 |
0,1821 |
|
18 |
0,1812 |
0,1585 |
0,1699 |
0,1680 |
|
19 |
0,1700 |
0,1567 |
0,1694 |
0,1702 |
|
20 |
0,1698 |
0,1664 |
0,1700 |
0,1600 |
Оцените статистическую управляемость процесса, предложите свои рекомендации по качеству его настройки и разбросу.
Х карта.
CL = ![]() = 0.1924
= 0.1924
![]() = 0.0286
= 0.0286
UCL=![]() +А2
+А2![]() = 0.1924+0.729*0.0286=0.2133
= 0.1924+0.729*0.0286=0.2133
LCL= ![]() –А2
–А2![]() =0.1924-0.729*0.0286=0.1716
=0.1924-0.729*0.0286=0.1716
R карта
CL=![]() =0.0286
=0.0286
UCL=D4![]() =2.282*0.0.286=0.0652
=2.282*0.0.286=0.0652
LCL=D3![]() =0*0.0286=0 – не определен
=0*0.0286=0 – не определен
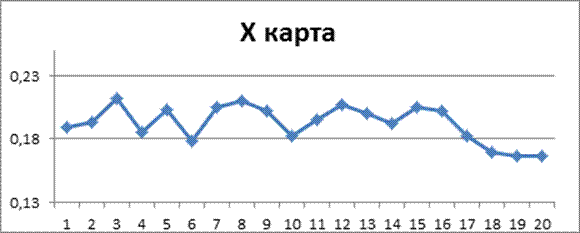
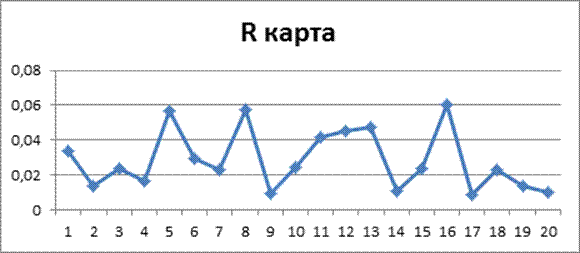
Вывод: По Х карте процесс статистически не управляемый. По R карте процесс статистически управляемый.
4. Для исследования коррозии цинка образцы, изготовленные в различных условиях, были подвергнуты климатическим воздействиям. В таблице 10 приведены результаты измерений десяти серий, по шесть образцов в каждой. Точность измерения 0,0001 дюйм.
|
№ п/п |
Измеренное значение |
|||||
|
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
Х6 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
0,5005 |
0,5000 |
0,5008 |
0,5000 |
0,5005 |
0,5000 |
|
2 |
0,4998 |
0,4997 |
0,4998 |
0,4994 |
0,4999 |
0,4998 |
|
3 |
0,4995 |
0,4995 |
0,4995 |
0,4995 |
0,4995 |
0,4996 |
|
4 |
0,4998 |
0,5005 |
0,5005 |
0,5002 |
0,5003 |
0,5004 |
|
5 |
0,5000 |
0,5005 |
0,5008 |
0,5007 |
0,5008 |
0,5010 |
|
6 |
0,5008 |
0,5008 |
0,5010 |
0,5005 |
0,5006 |
0,5009 |
|
7 |
0,5000 |
0,5001 |
0,5002 |
0,4995 |
0,4996 |
0,4997 |
|
8 |
0,4993 |
0,4994 |
0,4999 |
0,4996 |
0,4996 |
0,4997 |
|
9 |
0,4995 |
0,4995 |
0,4997 |
0,4992 |
0,4995 |
0,4992 |
|
10 |
0,4994 |
0,4998 |
0,5000 |
0,4990 |
0,5000 |
0,5000 |
Оцените результаты
анализа на коррозию с помощью (![]() -R)-карт
-R)-карт
Х карта.
CL = ![]() = 0.4997
= 0.4997
![]() = 0.00064
= 0.00064
UCL=![]() +А2
+А2![]() = 0.4997+0.483*0.00064=0.5
= 0.4997+0.483*0.00064=0.5
LCL= ![]() –А2
–А2![]() =0.4997-0.483*0.00064=0.4994
=0.4997-0.483*0.00064=0.4994
R карта
CL=![]() =0.00064
=0.00064
UCL=D4![]() =2.004*0.00064=0.0013
=2.004*0.00064=0.0013
LCL=D3![]() =0*0.00064=0 – не определен
=0*0.00064=0 – не определен
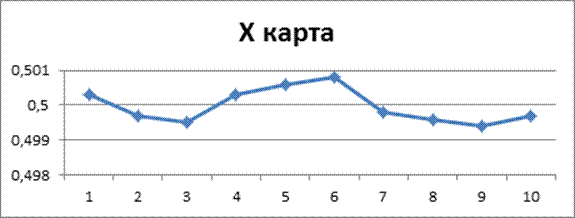
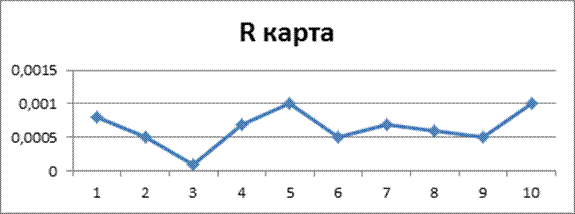
Вывод: по Х-карте процесс статистически не управляемый, а по R-карте статистически управляемый.
5. Контролировались защитные кожухи зубчатой передачи с гальваническим покрытием. Браковочным показателем являлись такие дефекты, как оголенные участки, грубое покрытие и т.п. Объем выборок был постоянным и равнялся 400. Результаты контроля выборок из 15 последовательно взятых партий представлены в таблице.
|
№ партии |
Число дефектных изделий |
№ партии |
Число дефектных изделий |
№ партии |
Число дефектных изделий |
|
1 |
1 |
6 |
0 |
11 |
2 |
|
2 |
3 |
7 |
1 |
12 |
0 |
|
3 |
0 |
8 |
0 |
13 |
1 |
|
4 |
7 |
9 |
8 |
14 |
0 |
|
5 |
2 |
10 |
5 |
15 |
3 |
Построить р-карту и оценить статистическую управляемость процесса.
СL=![]() =0.0055
=0.0055
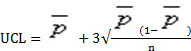 =0.0055+3
=0.0055+3![]() =0.01659
=0.01659
LCL=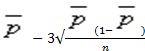 =0.0055-3
=0.0055-3![]() =-0.0056 – не определен
=-0.0056 – не определен
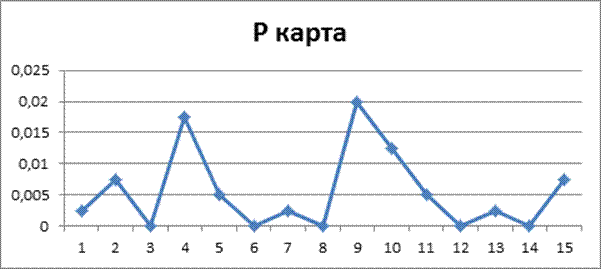
Вывод: процесс статистически не управляемый.
6. Ежедневно в течение 10 рабочих дней качество продукции контролируется по выборкам размером в 50 единиц. При этом получены следующие результаты
|
День |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Число бракованных изделий |
9 |
7 |
4 |
2 |
4 |
15 |
2 |
3 |
5 |
5 |
Постройте np-карту и проанализируйте статистическую управляемость процесса.
CL=n*![]() =50*0.0112=5.6
=50*0.0112=5.6
UCL=n*![]() +3
+3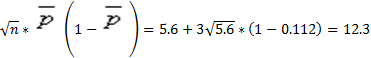
LCL=n*![]() +3
+3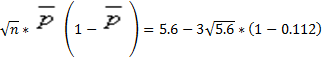 = - 1.1 – не определен.
= - 1.1 – не определен.
Вывод: процесс статистически не управляемый.
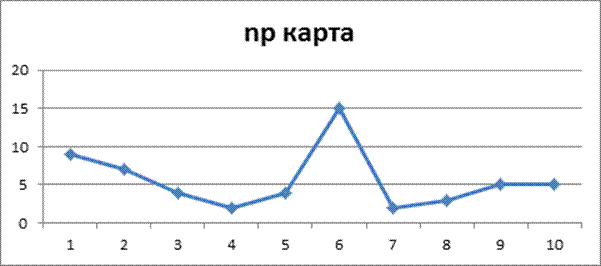
7. В таблице 13 приведены результаты контроля 25 последовательных партий холщовых мешков. Объем выборок был принят равным 10. Подсчитывались все дефекты, даже если встречались два или более одинаковых.
Таблица 13 - Результаты контроля холщовых мешков
|
№ выборки |
Число дефектов |
№ выборки |
Число дефектов |
№ выборки |
Число дефектов |
|
1 |
17 |
10 |
18 |
19 |
23 |
|
2 |
14 |
11 |
25 |
20 |
22 |
|
3 |
6 |
12 |
5 |
21 |
9 |
|
4 |
23 |
13 |
8 |
22 |
15 |
|
5 |
5 |
14 |
11 |
23 |
20 |
|
6 |
7 |
15 |
18 |
24 |
6 |
|
7 |
10 |
16 |
13 |
25 |
24 |
|
8 |
19 |
17 |
22 |
||
|
9 |
29 |
18 |
6 |
Построить С-карту и оценить статистическую управляемость процесса.
CL=![]() =15
=15
UCL=![]() +3
+3![]() =15+3
=15+3![]() =26.6
=26.6
LCL=![]() -3
-3![]() =15-3
=15-3![]()
Вывод: процесс статистически не управляемый.
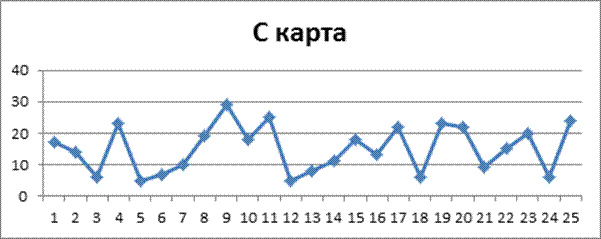
8. На заводе по производству шин каждые полчаса контролировали 15 шин и записывали общее число несоответствий.
|
№ выборки |
Число несоответствий с |
№ выборки |
Число несоответствий с |
№ выборки |
Число несоответствий с |
|
1 |
4 |
6 |
1 |
11 |
7 |
|
2 |
5 |
7 |
5 |
12 |
5 |
|
3 |
3 |
8 |
6 |
13 |
2 |
|
4 |
6 |
9 |
2 |
14 |
3 |
|
5 |
2 |
10 |
4 |
Построить u - карту и оценить статистическую управляемость процесса.
CL=![]() = 3.67
= 3.67
UCL= ![]() + 3
+ 3![]() = 5.15
= 5.15
LCL= ![]() - 3
- 3![]() = 2.18
= 2.18
Вывод: процесс статистически не управляемый.
9. Данные таблицы 15 представляют собой количество пробоев провода с резиновой изоляцией, измеряемого последовательными отрезками длиной 10000 см, при заданном испытательном напряжении.
|
№ отрезка |
Число пробоев, с |
№ отрезка |
Число пробоев, с |
№ отрезка |
Число пробоев, с |
|
1 |
1 |
8 |
6 |
15 |
16 |
|
2 |
1 |
9 |
1 |
16 |
20 |
|
3 |
3 |
10 |
1 |
17 |
1 |
|
4 |
7 |
11 |
10 |
18 |
6 |
|
5 |
8 |
12 |
5 |
19 |
12 |
|
6 |
1 |
13 |
0 |
20 |
4 |
|
7 |
2 |
14 |
19 |
При помощи контрольной с - карты оцените статистическую управляемость процесса изготовления провода. Если процесс статистически неуправляем, выполните корректирующие мероприятия и перестройте с - карту.
CL=![]() =6.2
=6.2
UCL=![]() +3
+3![]() =6.2+3
=6.2+3![]() =13.6
=13.6
LCL=![]() -3
-3![]() =6.2-3
=6.2-3![]()
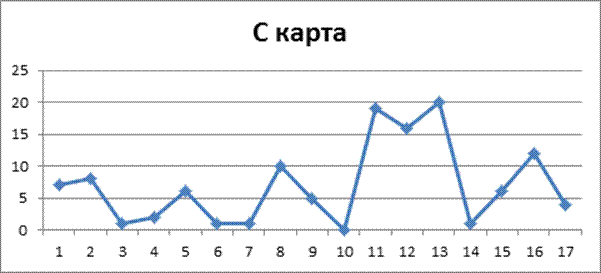
Вывод: Процесс статистически не управляемый.
После проведения корректирующих мероприятий было уменьшено число пробоев. Таким образом количество пробоев провода с резиновой изоляцией, измеряемого последовательными отрезками длиной 10000 см, при заданном испытательном напряжении стало следующим:
|
№ отрезка |
Число пробоев, с |
№ отрезка |
Число пробоев, с |
№ отрезка |
Число пробоев, с |
|
1 |
1 |
8 |
6 |
15 |
7 |
|
2 |
1 |
9 |
1 |
16 |
6 |
|
3 |
3 |
10 |
1 |
17 |
1 |
|
4 |
7 |
11 |
5 |
18 |
6 |
|
5 |
5 |
12 |
5 |
19 |
2 |
|
6 |
1 |
13 |
2 |
20 |
4 |
|
7 |
2 |
14 |
3 |
CL=![]() =3,45
=3,45
UCL=![]() +3
+3![]() =3,45+3
=3,45+3![]() =9,02
=9,02
LCL=![]() -3
-3![]() =3,45-3
=3,45-3![]()
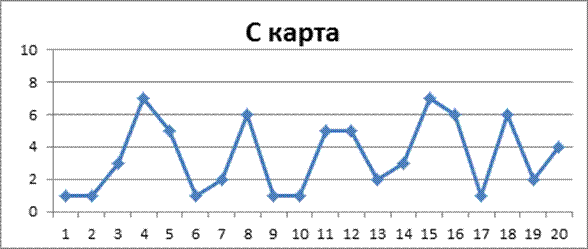
Вывод: после проведения корректирующих мероприятия процесс стал
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.