Построение выборочной функции распределения F(x) и гистограммы. Идентификация закона распределения (Отчет по расчетному заданию), страница 7

 - критерий Кочрена

Критическое значение критерия Кочрена  при

Так как G > 0.3682, то измерения неравноточные.

МНД:

Сравниваем  с критическим значением критерия Фишера и если гипотеза (Н₀) подтвердится, то ищем  - коэффициенты аппроксимирующего полинома, где S – ковариационная матрица:

p=1 – степень аппроксимирующего полинома

R=15811 – степень полинома превышает р (Н₀)

p=2 – степень аппроксимирующего полинома

R= 11795 – степень полинома превышает р (Н₀)

p=3  – степень аппроксимирующего полинома

R= 0.35622 – степень полинома не превышает р, так как критическое значение критерия Фишера = 3.5

А = [13.589      -10.093    -0.055126       1.5064] – коэффициенты аппроксимирующего полинома

Дисперсия оценки :

S_a =  0.26215       -0.024161      -0.014567        0.001713

       -0.024161      0.08157         0.001585        -0.0034475

       -0.014567      0.001585       0.0019062      -0.00031046

        0.001713     -0.0034475    -0.00031046    0.0001924  

Ковариационная матрица:

С = 32.079          0            0            0            0            0

            0        16.089         0            0            0            0

            0             0        5.091          0            0            0

            0             0            0       7.3533         0            0

            0             0            0            0       4.9945         0

            0             0            0            0            0       1.0431

p=k-1=6-1=5 – безизбыточная степень аппроксимирующего полинома

R= 3.6361e-024

A = [13.348      -10.108     0.048392       1.4968   -0.0040579   0.00046467]

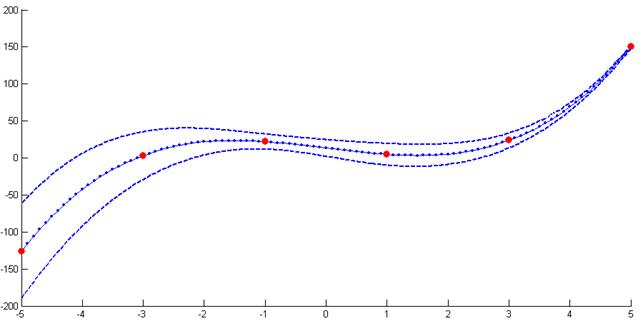
Рис. Аппроксимирующие полиномы 3 и 5 степеней, доверительный интервал для математического ожидания, математическое ожидание

Графики аппроксимирующих полиномов 3 и 5 степеней практически совпадают.