Математика \ Теория вероятностей

Построение выборочной функции распределения F(x) и гистограммы. Идентификация закона распределения (Отчет по расчетному заданию), страница 5

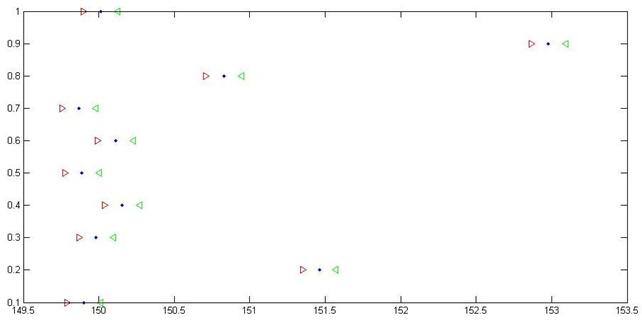
Рис. Интервальная оценка первого начального момента

Рис. Интервальная оценка второго центрального момента

Интерквантильный промежуток Jр для P=0.95 по всей выборке с помощью непараметрических толерантных пределов:

Jp=[ 115.82; 184.74] (k=90 и N-k=1910 элементы отсортированной выборки, где k находится из условия )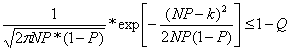

Интерквантильный промежуток Jр для P=0.95 по частичным выборкам с помощью параметрических толерантных пределов, считая закон распределения генеральной совокупности нормальным:

( где k- толерантный множитель )

+ - Jр по всей выборке с помощью непараметрических толерантных пределов

∙ - Jp для точечной оценки

>  < - Jp по частичным выборкам с помощью параметрических толерантных пределов

3. Идентификация закона распределения:

По значениям асимметрии и эксцесса, а так же по функции и плотности распределения делаем заключение, что это треугольное распределение (распределение Симпсона).

Проверим это гипотезу при значении уровня значимости по:

- критерию “Хи-квадрат”:

- теоретическая плотность распределения

- вероятность попадания значения в интервал

=19.172 - критерий

=25.989 – критическое значение критерия

Так как <, то делаем вывод, что гипотеза подтвердилась

- критерию Колмогорова-Смирнова:

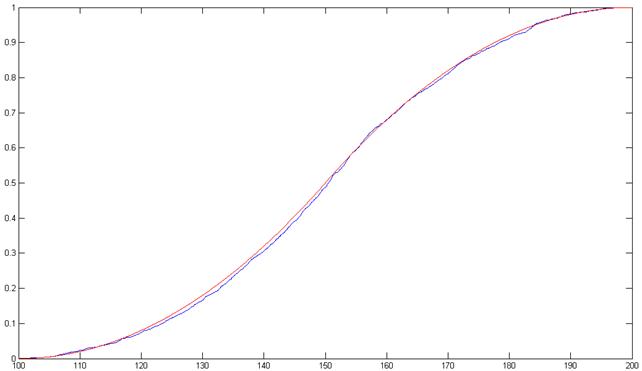
=0.025717 – максимальный модуль разности между предполагаемой функцией распределения и практически полученной функции распределения

= 0.027283 – критическое значение

Так как >D, то делаем вывод о том, что гипотеза верна.

- критерию Мизеса:

= 0.00016667 – расхождение между предполагаемой и выборочной функциями

=0.3473 – критическое значение критерия

Так как <, то делаем вывод о достоверности гипотезы.


Часть 2

Оценивание методом наименьших квадратов (МНК) и методом наименьшей дисперсии (МНД) коэффициентов полиномов, аппроксимирующих результаты измерений зависимых переменных.

В результате измерений при значениях независимой переменной

получены следующие данные:

Скачать файл