Представить эти же результаты графически точками на осях с указанием масштаба на этих осях по форме:
|

2.2. Интервальные оценки с доверительной вероятностью Q=0.8:
· первого начального и второго центрального моментов (вычисления выполнить по полной выборке и по отдельным частям, как в п. 2.1.4 - по N/10 значений в каждой частичной выборке).
· интерквантильного промежутка J для P=0.95:
o по всей выборке с помощью непараметрических толерантных пределов, симметричных и несимметричных относительно среднего арифметического
o по частичным выборкам с помощью параметрических толерантных пределов, считая закон распределения генеральной совокупности нормальным.
Результаты представить только графически аналогично тому, как описано выше – под графическим представлением соответствующей точечной оценки, предусмотрев для каждого варианта расчета отдельную ось.
Графическое представление толерантных пределов — также на отдельных осях для каждого варианта. Все оси обозначить.
3.
Идентифицировать закон распределения и выбрать подходящий
методом проб, определяя параметры закона (если моменты параметрами не являются)
и проверяя для КАЖДОЙ пробы гипотезу о соответствии предполагаемого закона
распределения экспериментальным данным с помощью ТРЕХ критериев:
"хи-квадрат", Колмогорова-Смирнова, "омега-квадрат".
Для начальной ориентировки в выборе закона использовать вид гистограммы, соотношения между моментами и полученные значения эксцесса и асимметрии. В отчете отобразить все ваши пробы относительно выбора подходящего закона распределения, а не одну последнюю (наиболее подходящую).
Подсказка к п.3 – возможные распределения:
Дискретные – биномиальное, геометрическое, гипергеометрическое, отрицательное биномиальное, Пуассона, равномерное
Непрерывные – арксинус, треугольное, Симпсона, Хи-квадрат, экспоненциальное, нормальное, равномерное, Стьюдента, бета, гамма.
Дано:
N = 2000;
Решение:
Из исходных данных получим вариационный ряд ( >> sort( X ) )
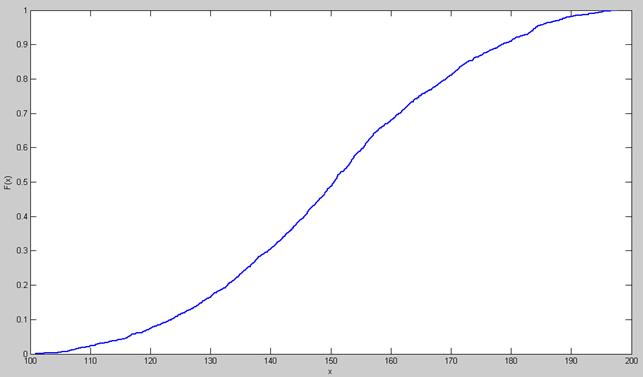
1.1 F(x) = P(x≤x) - выборочная функция распределения
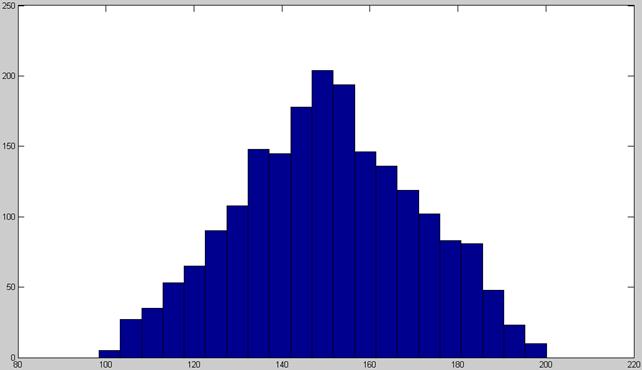
1.2 Гистограмма:
2.1 Примеры расчёта для полной выборки:
![]() - первый начальный момент (математическое ожидание,
среднее арифметическое)
- первый начальный момент (математическое ожидание,
среднее арифметическое)
![]()
![]() -
выборочная медиана
-
выборочная медиана
![]() -
середина размаха
-
середина размаха
![]() -
второй центральный
момент (дисперсия)
-
второй центральный
момент (дисперсия)
![]() -
среднеквадратическое значение (отклонение)
-
среднеквадратическое значение (отклонение)
![]() -
третий центральный
момент
-
третий центральный
момент
![]() -
четвёртый
центральный момент
-
четвёртый
центральный момент
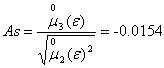 -
асимметрия
-
асимметрия
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.