Построение выборочной функции распределения F(x) и гистограммы. Идентификация закона распределения (Отчет по расчетному заданию), страница 6

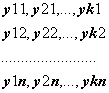
Выборочные значения находятся в файлах mnk_01.dat - mnk_10.dat.

Вычислить:

·  в каждой точке средние арифметические значения , оценки дисперсий , параметрические толерантные пределы для погрешностей, доверительные интервалы для математических ожиданий, проверить гипотезу о равенстве дисперсий в этих точках по критерию Кочрена;

·  оценки коэффициентов полинома МНК или МНД (в зависимости от исхода проверки гипотез о равенстве дисперсий)

·  проверить гипотезу о степени полинома, и если она не будет отвергнута, оценить дисперсии и ковариации оценок коэффициентов,

·  вычислить коэффициенты корреляции между оценками коэффициентов.

Внимание! Степень полинома a-priori не известна, поэтому необходимо начинать попытки аппроксимации с наименьшей степени и проверять гипотезу о степени полинома. При отклонении гипотезы увеличить степень аппроксимирующего полинома на единицу и проделать указанную процедуру вновь.

Приводить все промежуточные результаты, получаемые при каждой попытке.

Пусть гипотеза оказалась не отвергнутой при степени q. Тогда следует задать степень полинома равной k-1 и вновь вычислить оценки коэффициентов этого полинома и ковариационную матрицу оценок коэффициентов. Сопоставить с предыдущими результатами и прокомментировать возможное увеличение дисперсий оценок коэффициентов и ухудшение обусловленности задачи.

Представление результатов:

·  числовое - результаты, полученные на каждой итерации при каждом значении степени полинома q, в том числе, значения статистики критерия проверки степени полинома и критические значения критерия,

·  графическое - изобразить все точки, толерантные пределы и границы доверительных интервалов, средние значения и полученную аппроксимирующую полиномиальную функцию, причем эту функцию, границы доверительных интервалов и толерантные пределы соединить плавной линией; там же нанести функцию, полученную при безизбыточной аппроксимации полиномом степени k-1.

Средние арифметические значения:

Оценки дисперсий:

Параметрические толерантные пределы:

, где Р=0.95, Q=0.8

Доверительные интервалы для математических ожиданий:

, где Р=0.95, Q=0.8

x1	-125.99	32.079	-64.158	64.158	-190.15	-61.833
x2	3.2525	16.089	-32.179	32.179	-28.926	35.431
x3	22.003	5.091	-10.182	10.182	11.821	32.185
x4	4.7809	7.3533	-14.707	14.707	-9.9256	19.488
x5	23.656	4.9945	-9.9889	9.9889	13.668	33.645
x6	150.03	1.0431	-2.0863	2.0863	147.95	152.12