




Санкт–Петербургский Государственный Политехнический Университет
Факультет Технической Кибернетики
Кафедра Автоматики и Вычислительной Техники
ОТЧЕТ
о лабораторной работе № 4
по теме: Переходные процессы в линейных системах автоматического управления
Дисциплина: ТАУ
Выполнила студентка группы 3081/5
Грейбо Александр Владимирович
Руководитель: Бабко Леонид Васильевич
Санкт-Петербург
2009
1. Цель работы
Теоретическое изучение соотношений между входом и выходом, а также экспериментальное исследование линейных звеньев и систем с помощью переходных характеристик.
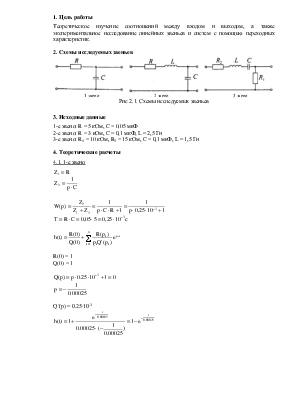
2. Схемы исследуемых звеньев

1 звено 2 звено 3 звено
Рис 2.1. Схемы исследуемых звеньев
3. Исходные данные
1-е звено: R = 5 кОм, C = 0,05 мкФ
2-е звено: R = 3 кОм, C = 0,1 мкФ, L = 2,5 Гн
3-е звено: R1 = 10 кОм, R2 = 15 кОм, C = 0,1 мкФ, L = 1,5 Гн
4. Теоретические расчеты
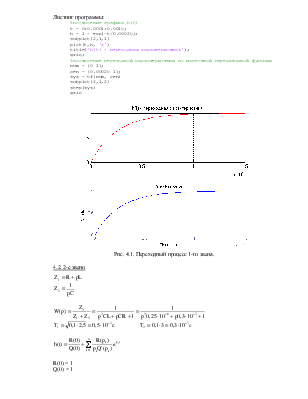
4.1. 1-е звено
![]()
![]()
![]()
![]()
![]()
R(0) = 1
Q(0) = 1
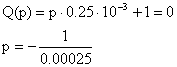
Q’(p) = 0.25∙10-3
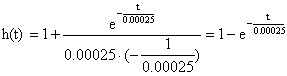
Листинг программы:
%построение графика h(t)
t = 0:0.0001:0.0015;
h = 1 - exp(-t/0.00025);
subplot(2,1,1)
plot(t,h, 'r')
title('h(t) - переходная характеристика');
grid;
%построение переходной характеристики по известной передаточной функции
num = [0 1];
den = [0.00025 1];
sys = tf(num, den)
subplot(2,1,2)
step(sys)
grid
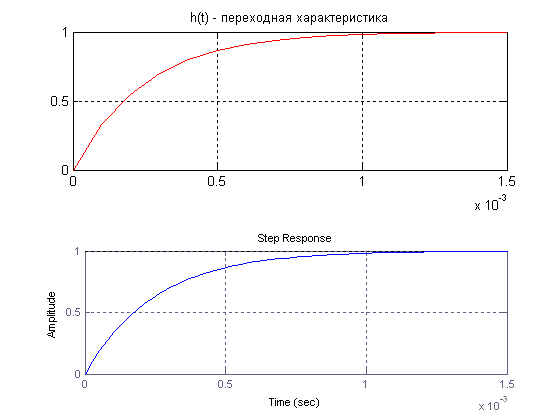
Рис. 4.1. Переходный процесс 1-го звена.
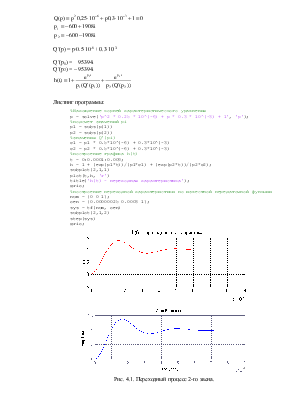
4.2. 2-е звено
![]()
![]()
![]()
![]()
![]()
R(0) = 1
Q(0) = 1
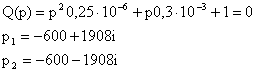
Q’(p) = p∙0.5∙10-6 + 0.3∙10-3
Q’(p1) = 95394i
Q’(p2) = – 95394i
![]()
Листинг программы:
%Нахождение корней характеристического уравнения
p = solve('p^2 * 0.25 * 10^(-6) + p * 0.3 * 10^(-3) + 1', 'p');
%подсчет значений pi
p1 = subs(p(1))
p2 = subs(p(2))
%значения Q'(pi)
q1 = p1 * 0.5*10^(-6) + 0.3*10^(-3)
q2 = p2 * 0.5*10^(-6) + 0.3*10^(-3)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.