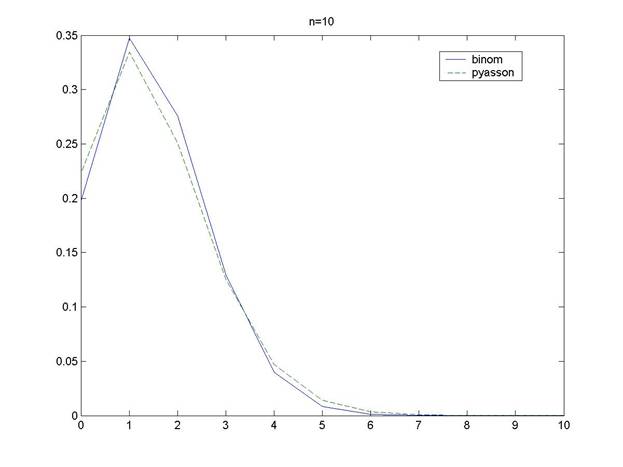
>> n=10;
>> np=1.5;
>> N=1;
>> M=np/n;
>> P=[];P1=[];
>> for m=0:1:10
i=m;
P(i+1)=binom(n,i,M,N);
end
>> for m=0:1:10
i=m;
P1(i+1)=pyasson(n,i,M,N);
end
>> plot(0:1:10,[P ;P1])
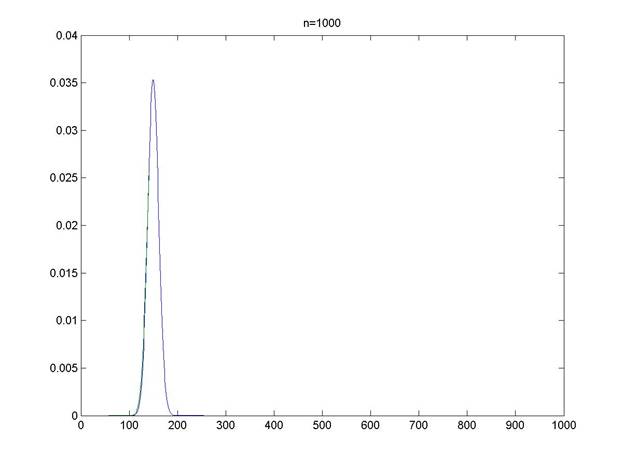
>> n=1000;
>> for m=0:1:1000
i=m;
P(i+1)=binom(n,i,M,N);
end
>> for m=0:1:1000
i=m;
P1(i+1)=pyasson(n,i,M,N);
end
>> plot(0:1:1000,[P ;P1])
function p=norm(n,p,k)
% Входные параметры:
% n-количество испытаний
% p-вероятность появления события
% k-количество появлений события
q=1-p;
x=(k-n*p)/sqrt(n*p*q);
f=1/sqrt(2*pi)*exp((-x^2)/2);
p=1/sqrt(n*p*q)*f;
>> P=[];P1=[];
>> for m=0:1:10
i=m;
P(i+1)=normal(10,0.3,i);
end
>> N=1;
>> M=0.3;
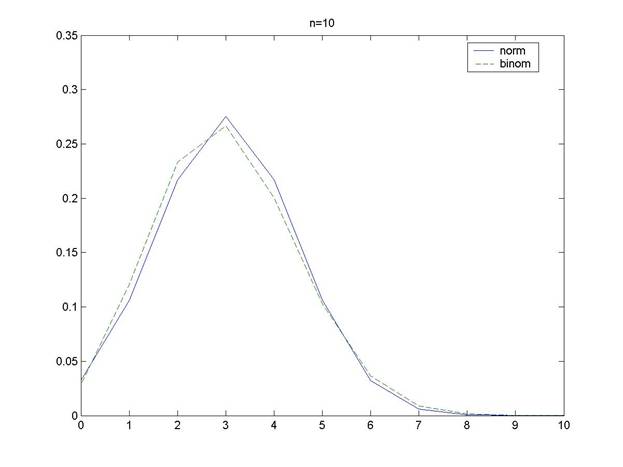
>> n=10;
>> for m=0:1:10
i=m;
P1(i+1)=binom(n,i,M,N);
end
>> plot(0:1:10,[P ;P1])
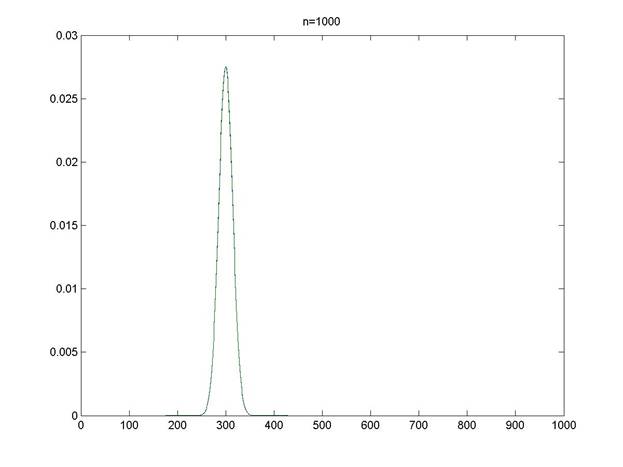
>> n=1000;
>> P=[];P1=[];
>> for m=0:1:1000
i=m;
P(i+1)=binom(n,i,M,N);
end
>> for m=0:1:1000
i=m;
P1(i+1)=normal(1000,0.3,i);
end
>> plot(0:1:1000,[P ;P1])
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.