2) используется дополнительный модифицированный код как в АЛУ, так и в ОЗУ;
3) числа n+2 разрядные: n+1 и n+2-ой разряды отведены под знак, кодируемый 00 – «+»; 11 – «-».
Далее как правило не будут специально не оговариваться тип используемого сумматора, поскольку в конечном счете это не особо существенно ввиду включения ныне в процессор большого числа регистров. Пусть для определенности используется комбинационный сумматор на два многоразрядных входа.
Рис. 2.2.2.1.
Работа очень легко может быть пояснена с помощью структурной схемы алгоритма:
Рис. 2.2.2.2
На рисунке обозначен БФПР – блок формирования признаков результата. Он состоит из комбинационной схемы и регистра признаков (РгПр).
Помимо сигнала завершения операции ![]() БФПР формирует еще:
БФПР формирует еще:
− переполнение разрядной сетки - Q;
− обнуление разрядной сетки - Z;
− результат больше или меньше 0 – N;
− число «1» в результате четно - Р - или нечетно и, возможно, другие признаки результата.
Просты и соответствующие выражения:
![]() ;
;
![]() ;
;
![]()
и т.д.
Все эти признаки потенциально будут использоваться УУ для формирования очередного адреса (следующая команда, условный переход, прерывание по переполнению и т.д.)
<91>
2.2.3. Организация АЛУ (параллельного действия) в режиме умножения чисел с фиксированной запятой.
Сначала обзор-напоминание.
Умножение двоичных чисел с фиксированной запятой сводится к последовательности сложений и сдвигов: произведение суть сумма частичных произведений, каждое из которых получается умножением множимого на один разряд множителя.
Но умножение на разряд двоичного числа – это уже почти не умножение, ибо умножаем здесь мы на «0» или «1».
Произведение двух n-разрядных чисел составляет до 2n разрядов:
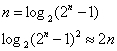
<92>
Известно, что в зависимости от порядка просмотра множителя и способа формирования суммы частичных произведений различают четыре способа организации умножения.
Рассмотрим их с точки зрения размещения в регистрах АЛУ.
Первый способ. Умножение младшими разрядами (множителя) вперед со сдвигом суммы частичных произведений вправо. Если мы сдвигаем сумму частичных произведений, то куда? Нужно увеличивать число разрядов сумматора? – Нет! Нет по двум причинам:
младшие (выдвигаемые) разряды далее не меняются;
поскольку множитель также сдвигается вправо, то в регистре, где он «сидит», старшие разряды освобождаются.
Итак, возможно размещение младших разрядов суммы вдвиганием их в регистр множителя. Заметим здесь, что такая схема удобна и при выполнении операции деления.
Регистр множителя и сумматор обязаны иметь цепи сдвига содержимого вправо. Для регистра множимого этого не нужно. Младший разряд сумматора (регистра) частичных произведений должен быть соединен по цепям со старшим разрядом регистра множителя.
Рис. 2.2.3.1.
На каждом шаге выполнения умножения определяется содержимое младшего разряда Рг множителя. Если в нем «1», то к сумме частичных произведений добавляется множимое. Затем производится одновременный сдвиг. При «0» в младшем разряде Рг множителя добавления нет, а сдвиг такой же. В конце умножения (заметим, что этот «конец» надо поймать) старшие разряды произведения «лежат» в См, а младшие в Рг множителя.
Поскольку метод значительно экономит оборудование (всего необходимы три одинаковых n-разрядных регистра), то он чаще всего в ЭВМ и применяется.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.