Анализ нагруженности плоского рычажного механизма, страница 5

С учетом векторного уравнения (1.3.5) строим замкнутый силовой многоугольник. На плоскости чертежа выбираем полюс . От него проводим вектор произвольной длины по направлению силы . Вычисляем масштабный коэффициент  по формуле:

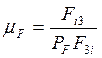                                (1.3.6)

=1,0 (Н/мм)

Далее к вектору  достраиваем в произвольном порядке другие составляющие уравнения (1.3.5), рассчитывая длину векторов при помощи масштабного коэффициента. 

Для  расчета  группы  2-4  нужно  приложить  силу   , равную  по  модулю  силе   и  противоположно  направленную.        

Реакции  в  шарнирах  нужно  разложить  на  составляющие  по  направлению  осей    и  , и  перпендикулярным  им   и  .  Тангенциальные  составляющие  можно  найти,  если  записать  уравнение  можно  найти, если  записать  уравнение  суммы  моментов  каждого  звена.

Условие  равновесия  звена  2:

                                 (1.3.8)

отсюда:

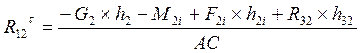                                       (1.3.9)

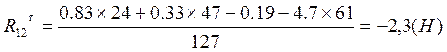
условие  равновесия  4: 

                  (1.3.10)

отсюда:                                                                                                                                                                       

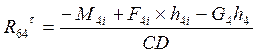               (1.3.11)

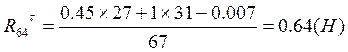
Рассматривая  уравнение  равновесия  группы  в  целом, можно  увидеть, что  неизвестные  силы    и  . Векторное  уравнение  равновесия  этой  группы  будет  иметь  вид :

                           (1.3.12)      (1.3.12)  В  этом  уравнении  известны  все  составляющие 

Масштабный  коэффициент   

Теперь определим  уравновешивающую силу и уравновешивающий момент,  действующий на кривошип ОА. В этом случае уравнение моментов всех сил, приложенных к кривошипу относительно точки В, имеет вид

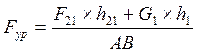                                                           (1.3.13)

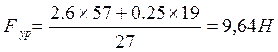
Уравновешивающий момент определяется по формуле:

             (1.3.15)

Рассматривая  уравнение  ведущего звена, можно  увидеть, что  неизвестна  сила  . Векторное  уравнение  равновесия  этой  группы  будет  иметь  вид:

F_ур+F_1i+G₁+R₂₁₊ R₆₁=0;

С учетом векторного уравнения (1.3.5) строим замкнутый силовой многоугольник. На плоскости чертежа выбираем полюс . От него проводим вектор произвольной длины по направлению силы . Вычисляем масштабный коэффициент  по формуле:

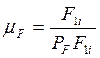                                (1.3.6)

=1,0 (Н/мм)

Далее к вектору  достраиваем в произвольном порядке другие составляющие уравнения (1.3.5), рассчитывая длину векторов при помощи масштабного коэффициента. 

Все найденные при силовом анализе величины  представлены в таблице 3.1.

Таблица 3.1–Силы и моменты, действующие на механизм

2.Проектный расчет звена механизма на прочность

2.1.Определение проекции сил, действующих на звено.

В результате динамического анализа плоского рычажного механизма были определены внешние силы, которые действуют на каждое звено и кинематическую пару. Такими внешними усилиями являются силы инерции F_i, моменты инерции М_i. Под действием внешних сил звенья плоского механизма деформируются. Для данного плоского рычажного механизма преобладающими являются составляющие деформации изгиба и растяжения. Анализ нагруженности группы Ассура 2–4 показывает, что звено 2 во время работы механизма получает общее действие на него изгибания и растяжения. На стадии проектирования механизма важно дать оценку прочности его элементов. Для этого определим с помощью метода сечений величину внутренних усилий, что действуют в сечениях элементов рычажного механизма. Все силы, действующие на звено 4 группы 2-4 переносим в точку С и определяем их значение с учетом угла их направления относительно звена АС. Значения всех проекций всех сил заносим в таблицу 2.1.