Механика \ Техническая механика

Анализ нагруженности плоского рычажного механизма, страница 2

VA =wВА lBA                                                              (1.2.2)

где  lBA - длина  звена  AB,  в  метрах 

Находим  скорость  точки  А:

*   = 73,260,03 = 2,19 ()

Направление  вектора    перпендикулярно  звену  АВ  в  направлении  его  вращения.

Из  произвольно  выбранной  точки   pv откладываем  вектор  произвольной  длины,   численно  равный  вектору  скорости  .  Определяем  масштабный  коэффициент  скорости по  формуле:                                 

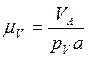                                           (1.2.3)        

где    - истинная  скорость  точки  А,  м / с;  

pv а-  длина  вектора    в  мм.

Масштабный  коэффициент  скорости  равен:                                                                                                      

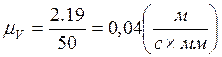                                                                                          Для  определения  скорости  точки  С  воспользуемся  условием принадлежности  точки  С  одновременно  двум  звеньям:  АС  и  DC.  Рассматривая  движение  каждого  из  этих  звеньев  как  плоско-паралельное,  запишем

VC =VA +VCA                                                                    (1.2.4)          

VC =VD +VCD                                                                     (1.2.5)           где  VCA  - скорость  точки  C  вокруг  точки  А,

VCD  -  скорости  точки  C  вокруг  точки  D.

Величину   и  направление скорости точки  C  можно  определить   только совместным  решением  этих  двух  векторных  уравнений. В уравнении (1.2.4)первое слагаемое VA  известно по величине и направлению, а о скорости VCA известно только то, что она перпендикулярна  звену   АC. Поэтому для построения векторной суммы необходимо  к  концу  вектора  VA  провести  линию,  перпендикулярную  звену   АC. В уравнении (1.2.5)первое слагаемое VC  равно нулю так как точка D неподвижна. Из полюса pv проводим вектор нулевой длины. Другому составляющему – VCD на плане скоростей  соответствует линия, проходящая через точку С перпендикулярно  звену   СD. Точка с будет находится на пересечении линий скоростей VCA и  VCD .

Определим  абсолютное значение  VC:        

 VC = pvс×                                                                 (1.2.6)             где pvс -  длина  вектора    VC     в  мм

VС=32  0,04 = 1,37 (м/с)

Точка е на плане скоростей находится в одной точке с точкой S2 , находится по формуле:

Определяем  истинное  значение  VЕ:

 VЕ = pvе×                                                                    (1.2.8)

где  е - длина  вектора  VЕ  в  мм

VЕ =400,04=1,72(м/с)                       

Условие  принадлежности  точки  F    звену EF дает векторное уравнение:

VF =VE +VFE, где  VFE  - скорость  точки  F  вокруг  точки  E.

В этой векторной сумме неизвестно второе составляющее - VFE. О нем известно только то что линия действия этого вектора перпендикулярна звену EF. Соответствующую линию проводим на плане скоростей через точку е. Для того, чтобы составить второе уравнение для скорости VF, на неподвижной направляющей выделяем точку F0 .Тогда скорость VF будет равна:

VF =VF0 +VFF0;

Скорость точки F0 равна нулю, а скорость VFF0 направлена вдоль движения ползуна. Точка f будет находится на пересечении линий направления скоростей VFF0 и VFE. Численное  значение  VF:

 VF = pvf×,                                                                   (1.2.8)

где  pvf - длина  вектора  VF  в  мм:

VF=0,04 ×19=0,817 (м/с) .                                  

Полученный план скоростей позволяет не только определить   скорости всех точек механизма,  а также величину и направление всех  скоростей звеньев. Все линии плана, исходящие из точки , представляет собой абсолютные скорости точек. Периферийные линии - относительные скорости звеньев.  Для нахождения  VCA используют план скоростей:

VCA =аc(1.2.10)

где  ав–длинна  VCAна плане скоростей

VCA =300,04=1,2(м/с).

Угловую скорость звена АС  находим по формуле:

Скачать файл