Анализ нагруженности плоского рычажного механизма, страница 4

- тангенциальная составляющая ускорения точки F в ее относительном движении вокруг точки E. Для того, чтобы составить второе уравнение для ускорения точки F, на неподвижной направляющей выделяем точку F₀ .Тогда ускорения точки F будет равно:

                                                          (1.2.16)

Ускорение точки F₀ равно нулю, а ускорение а_FF0 направлено вдоль движения ползуна. Точка  будет находиться на пересечении линий направления ускорений а_FF0 и . Численное  значение  а_F:

 ,                                        (1.2.9)

(м/c²)                                 

Для  определения  величины  углового  ускорения  звена  используем  зависимость:                                                                        

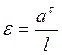                                                           (1.2.26)

где         –  тангенциальное ускорение этого звена, м/с

l - длина звена, м

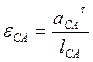                                                                                            (1.2.27)

Все полученные при построении плана ускорений ускорения точек и угловые ускорения звеньев приведены в таблице 1.2.2

Таблица 1.2.2 – Ускорения точек и угловые ускорения звеньев механизма.

продолжение

Масштабный коэффициент плана ускорений =3.22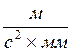

1.3      Кинетостатический анализ механизма

1.3.1.Определение сил инерции механизма.

Кинетостатический расчет положенный в основу силового расчета механизма базируется на принципе Д’Аламбера Если к механизму кроме внешних сил приложить силы инерции его звеньев, то условно можно считать, что механизм находится в равновесии. В этом случае для определения реакций в кинематических парах можно использовать уравнения статики, если в них включить силы инерции звеньев.

Сила инерции звена направлена в сторону, противоположную направлению ускорения центра масс этого звена и равна произведению массы этого звена на ускорение центра масс:

                                     (1.3.1)

При этом существует также главный момент инерции звена, который приложен к центру масс звена и направлен в противоположную угловому ускорению звена сторону. Определяется по формуле:

                                               (1.3.2)

где - момент инерции звена для стержневого механизма 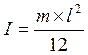, кг м

  - угловое ускорение звена,

Силы и главные моменты инерции механизма приведены в таблице 1.3.1

Таблица 1.3.1.- Рассчитанные  значения сил и моментов инерции звеньев механизма.

1.3.2 Определение реакций в кинематических парах.

Силовой анализ механизма начинается с группы Ассура 3-5 , наиболее удаленной от ведущего звена. Связи в шарнирах заменяются реакциями . Реакция в шарнире Е не известна ни по модулю, ни по направлению, поэтому нужно разложить ее на составляющие: по направлению оси    и перпендикулярно ей  ; реакция  также неизвестна по модулю, но известна по направлению. Обозначим в точке    направление силы инерции и аналогично силу инерции в точке . Тангенциальные  составляющие  можно  найти,  если  записать  уравнение  суммы  моментов  для  звена EF.     Условие  равновесия  звена:

                                  (1.3.3)

из которого находим

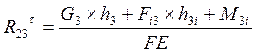
                                     (1.3.4)

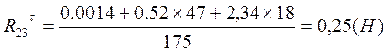
Составляем векторное уравнение:

                                     (1.3.5)