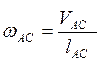Анализ нагруженности плоского рычажного механизма, страница 3

                                                                       (1.2.11)

где l_AC- длина звена АВ

V_CA - относительная скорость C вокруг А:

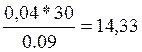=(рад/с).

Аналогично для звена  CD:

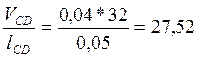 =(рад/с).                                     

Аналогично для звена  EF

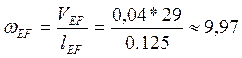 (рад/с).                                     

Все найденные скорости точек и звеньев механизма, угловые скорости приведены в таблице  1.1

Таблица 1.1– Скорости точек и звеньев механизма, угловые скорости.

VA м/с	VC м/с	VЕ м/с	VAC м/с	VF м/с	с-1	с-1	с-1	=0,04()
2,19	1,37	1,72	1,2	0,817	14,33	27,52	9,97

Продолжение

VS1 м/с	VS2 м/с	VS3 м/с	VS4 м/с	VS5 м/с
1,075	1,72	0,989	0,688	0,817

1.2.2. Определение ускорений точек и звеньев механизма.

Для определения ускорений точек применяем метод планов ускорений. Построение планов ускорений начинаем с ведущего звена механизма. Поскольку задано, что  угловая  скорость  ведущего  звена -  величина  постоянная,  то ускорение  точки  А  вычисляем  по  формуле:    

                                                                          (1.2.13)

где  - длина звена ВА

= (м/с²)

Ускорение точки А  направлено вдоль звена ВА к центру его вращения, т.е. в данном случае ускорение точки А равно её  нормальной составляющей. Из  произвольно выбранной точки π_а чертежа откладываем вектор π_а произвольной длины, численно равный вектору ускорения точки А.  Определение  масштабного коэффициента плана ускорений производится следующим образом:

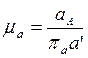                                                                    (1.2.14)

где - длина вектора в мм.

()

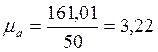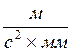Для определения ускорения точки С воспользуемся условием принадлежности точки одновременно двум звеньям АC и DC.

Рассматривая движение каждого из этих звеньев как плоскопараллельное движение твердого тела, из условия двойной принадлежности точки C имеем:

                                                (1.2.15)

                                                (1.2.16)

где  - нормальная составляющая ускорения точки C в её относительном движении вокруг точки А;

- тангенциальная составляющая ускорения точки C в ее относительном движении вокруг точки А;

- нормальная составляющая ускорения точки C в её относительном движении вокруг точки D;

- тангенциальная составляющая ускорения точки C в ее относительном движении вокруг точки D;

Величину   можно  определить  из  плана скоростей:

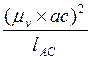=  =           (1.2.17)

==18,49(м/c² )

а его длина на плане  ускорений считается с учетом масштабного коэффициента  по формуле:

=          (1.2.18)

==5,74 (мм)

Данный вектор направлен вдоль звена АC от точки C к точке  А. Графически решить уравнение – значит, прибавить к концу вектора  вектор, параллельный звену АC, направленный от C к А, длиной , а из конца последнего  провести линию, перпендикулярную звену АC, которая  представляет собой линию действия вектора тангенциального ускорения , неизвестного по величине.

Величина ускорения и  его длина на плане ускорений определяются по формулам, аналогичным (2.17) и (2.18)

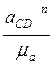=                                                           (1.2.19)

= =11,7  (мм)

Точка пересечения  линий действия векторов  и  дает ускорение точки C:

                                                          (1.2.20)

=3.2245=144,9(м/с²)

Численное значение ускорения точки Е находим по формуле:      

                                                (1.2.21)  

(м/c²)                                

Условие  принадлежности  точки  F    звену EF дает векторное уравнение:

                                                (1.2.16)

где  - нормальная составляющая ускорения точки F в её относительном движении вокруг точки E;