Методы и средства автоматического контроля, страница 10

Разряды X	Середина разряда Xi	Частота f	Частость mx
0.02-0.027	0.0235	3	3/100
0.027-0.034	0.0305	7	7/100
0.034-0.041	0.0375	27	27/100
0.041-0.048	0.0445	19	19/100
0.048-0.055	0.0515	26	26/100
0.055-0.062	0.0585	9	9/100
0.062-0.069	0.0655	8	8/100

Вычисление статистических характеристик распределения

Разряды Х	Середина разряда Xi	Частота f	B=(Xi-a)/c	B∙f	B2∙f
0.02-0.027	0.0235=a	3	0	0	0
0.027-0.034	0.0305	7	1	7	7
0.034-0.041	0.0375	27	2	54	108
0.041-0.048	0.0445	19	3	57	171
0.048-0.055	0.0515	26	4	104	416
0.055-0.062	0.0585	9	5	45	225
0.062-0.069	0.0655	8	6	48	288

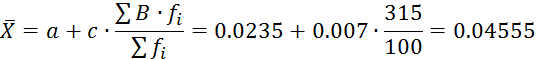
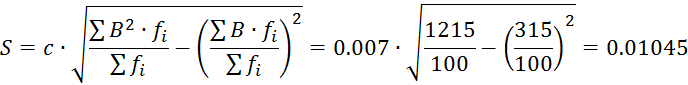
Для вычисления моментов составляют вспомогательную таблицу.

Вспомогательные данные для вычисления моментов.

Хi	fi	Bi	Bi∙fi	Bi2∙fi	Bi3∙fi	Bi4∙fi	Bi+1	(Bi+1)4∙fi
0.0235	3	0	0	0	0	0	1	3
0.0305	7	1	7	7	7	7	2	112
0.0375	27	2	54	108	216	432	3	2187
0.0445	19	3	57	171	513	1539	4	4864
0.0515	26	4	104	416	1664	6656	5	16250
0.0585	9	5	45	225	1125	5625	6	11664
0.0655	8	6	48	288	1728	10368	7	19208

     

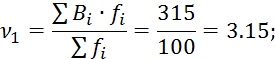
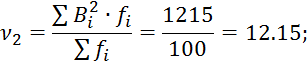
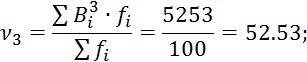
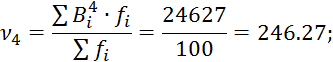
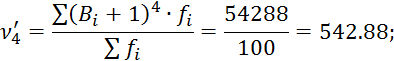
Для проверки правильности вычисления центральных моментов определяем μ₃ и μ₄ по следующим зависимостям:

Пользуясь моментами вычисляем статистические характеристики распределения и сравниваем с полученными в первой части работы.

Учитывая, что центральный момент 2-го порядка представляет собой дисперсию случайной величины Х, получаем:

На практике встречаются отклонения, которые отклоняются от нормального. С помощью моментов мера асимметрии вычисляется по формуле:

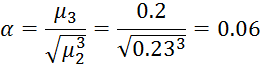
Если α > 0, то мера асимметрии положительная;

Если α < 0, то мера асимметрии отрицательная;

Если α = 0, то асимметрия отсутствует.

Эксцесс

Если τ > 0, то вершина кривой распределения лежит выше нормальной, эксцесс – положительный.

Если τ < 0, то вершина кривой распределения лежит ниже нормальной, эксцесс – отрицательный.

Если τ = 0, то кривая нормальная, эксцесс – отсутствует.

В данном случае α > 0, следовательно мера асимметрии положительная, τ < 0, эксцесс –отрицательный. 

Литература

1.       Белоусов А.П., Дащенко А.И., Полянский П.М., Шулешкин А.В. «Автоматизация процессов в машиностроении».  Учебное пособие для вузов. Москва, «Высшая школа», 1973 г., - 456 с., ил.

2.       Педь Е.И. «Активный контроль в машиностроении». Москва, «Машиностроение», 1971 г., - 360 с.

3.       Высоцкий А.В., Курочкин А.П. «Пневматические средства измерений линейных величин в машиностроении». Москва, «Машиностроение», 1979 г.,  - 206 с., ил.

4.       Косиловой А.Г., Мещерякова Р.К. «Справочник технолога-машиностроителя». Т.1, Т.2. Москва, «Машиностроение», 1985 г., - 656 с., -496 с., ил.

5.       Положий П.С., Методические указания к практическому занятию «Определение погрешностей обработки, вызываемых тепловыми деформациями технологической системы»: Учебное пособие – высшая школа, 1990 г., - 64 с