Построение аддитивной модели тренда и сезонности для прогнозирования прибыли предприятия

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ДОНБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Факультет экономики и финансов

Кафедра финансов

Индивидуальное задание №4

по дисциплине: "Статистика финансов и банковского дела"

Вариант 11

                                                                             Выполнила: ст.гр. ФН-04-2

Листопад Е.П.

                                                                             Проверила: Чабаненко И.Л.

Алчевск, 2008

На основе данных, скорректированных на инфляцию, о прибыли компании за 12 кварталов (табл. 2.1) построить аддитивную модель тренда и сезонности для прогнозирования прибыли компании на следующие два квартала. Дать общую характеристику точности модели и сделать выводы.

Таблица 2.1 - Прибыль компании (тыс. грн.)

Год	1996				1997				1998
Квартал	I	II	III	IY	I	II	III	IY	I	II	III	IY
Прибыль	160	130	159	165	156	141	157	172	157	145	163	177

Решение

Шаг 1. Выявление наличия тенденции и сезонности. Определение вида модели для анализа и прогноза.

Идентифицируем переменные:

у(t) - фактические значения квартальной прибыли;

t     - порядковый номер квартала.

Построим диаграмму фактических данных и определим вид модели для анализа и прогноза (рис.2.1).

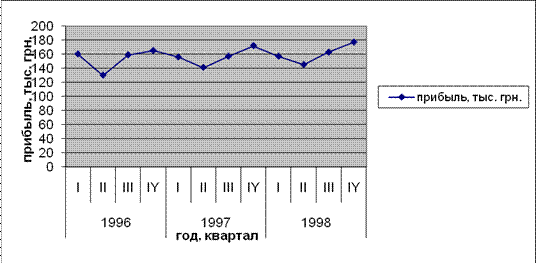
Рисунок 2.1 - Фактическое значение прибыли компании по кварталам

Из диаграммы следует, что возможен возрастающий тренд, содержащий сезонные колебания. Величина прибыли в IY квартале значительно выше, чем в  I, II и III кварталах. Сезонная компонента колебания практически не изменяется в течение 3-х лет. Тренд показывает, что в целом величина прибыли возросла со 160 тыс. грн. до  177 тыс. грн., однако, увеличения сезонных колебаний не произошло. К таким данным следует применять аддитивную модель: . Уравнение  будет оценкой этой модели.

Шаг 2. Расчет  значений сезонной компоненты.

Для того чтобы элиминировать влияние сезонной компоненты воспользуемся методом скользящей средней.