Проецирование геометрических фигур

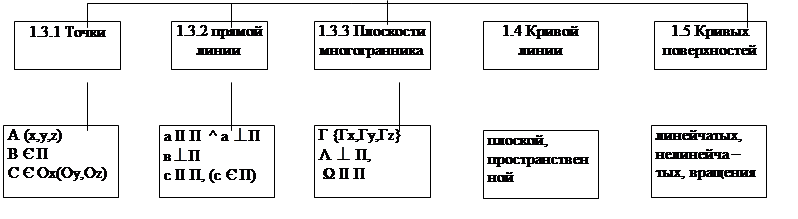
1.  Проецирование геометрических фигур

1.1.  Метод проекций

При проектировании зданий и сооружений , машин и механизмов , применяются различные виды проекций, дерево которых показано на рис.1.1

     Всякий объект трёхмерного мира (евклидова пространства) можно представить множеством точек, которые могут быть изображены на плоскости  (чертеже). Геометрический объект (включая точку, линию, плоскость, поверхность) как точечное множество, отображается на плоскость чертежа по законам проецирования.

      Метод проекций заключается в проведении через все точки объекта проецирующих лучей s до пересечения с плоскостью проекций П. Точки пересечения образуют изображения фигуры, т.е. её проекцию (Рис.1.2).

     1.1.1 При центральном проецировании (см. рис.1.2а) центр проекций S не должен совпадать с плоскостью проекций П, а проецируемая  фигура [AB] может находиться перед плоскостью и за ней.

    1.1.2При параллельном проецировании (см. рис.1.2б) центр S удалён в бесконечность, а проецирующие  лучи, параллельны заданному направлению проецирования s. При ортогональном проецировании (см. рис.1.2в) угол  между проецирующим лучом и плоскостью проекций – прямой. Параллельные проекции – это частный случай центрального проецирования, а ортогональные – частный случай параллельного проецирования.

   1.1.3 Геометрические фигуры проецируются на плоскость в общем случае с искажением линейных и угловых величин. Однако между оригиналом и его проекцией существует определенная связь и некоторые его свойства остаются без изменения (называемые «инвариантами проецирования»).

            1. Проекция точки есть точка: в символьной форме:  А ÞA₁

               2. Если фигура 1 принадлежит фигуре 2, то и проекция фигуры 1

принадлежит проекции фигуры 2 : ( 1Ф Є 2Ф Û 1Ф₁ Є 2Ф₁ );

               3. Плоская фигура, параллельная плоскости проекций, проецируется на эту плоскость в конгруэнтную (равную) фигуру:(Ф║П Û Ф₁≡Ф);

Из этих основных свойств следует:

          1a. Проекция множества есть множество: ( N Þ N₁ );

1б. Проекция прямой в общем случае – прямая линия: ( l Û l₁ );

 1в. Проекция прямой , проходящей через центр S или параллельной направлению проецирования s, есть точка: ( l ^ П Û l₁ ≡ L );

1.1 Метод  проекций

1.1.1 Центральное проецирование

1.1.2 Параллельное проецирование

                       

		1.2.3 Перспективные проекции на 1 плоск. (см.п.9)			1.2.1 Прямоугольные (ортогональные) проекции		1.2.2.Косоугольные проекции
		1.2.4 С числовыми отметками (см.п.8)			1.3 Ортогональные на 2-3 плоскости		Аксонометрические на 1 плоскость (см. п. 4)
			Рис 1.1.  Дерево метода проекций

 

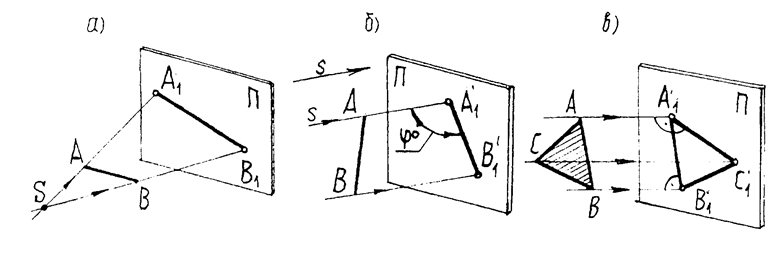
Рис 1.2  Метод проекций: а – центральное проецирование; б – параллельное        проецирование по направлению s; в – прямоугольное (ортогональное) проецирование.

1г. Проекция плоской фигуры, проходящей через центр S или параллельной направлению проецирования, есть линия: (Ф Є α ^ Ф ^ П Û Ф₁ ≡ l₁ );

          2a. Если точка принадлежит прямой, то ее проекция принадлежит проекции прямой: ( А Є l Û A₁ Є l₁ );

          2б. Если точка принадлежит линии и линия принадлежит поверхности

( плоскости ), то проекция точки принадлежит проекции поверхности

( плоскости ): ( А Є l Є Г Þ A₁ Є Г₁ );

          2в.Пересекающиеся  прямые  проецируются  пересекающимися прямыми, при этом точка пересечения прямых проецируется в точку пересечения проекций прямых: ( а ∩ в = К  Û  а₁ ∩ в₁ = К₁ );

          2г. Любые пересекающиеся объемные фигуры А и В проецируются плоскими фигурами, при этом фигура пересечения l проецируется в плоскую фигуру l₁ пересечения проекций: ( A ∩ B =l Û A₁ ∩ B₁  = l₁).

        Дополнительно для параллельного проецирования:

          1д. Проекции параллельных прямых параллельны: ( a ║ b Û a₁ ║ b₁ ).

          2д. Отношения проекций отрезков одной или двух параллельных прямых равно отношению этих отрезков: