Проецирование геометрических фигур, страница 4

                 1.4.   Ортогональные проекции кривых линий

      1.4.1.  Кривую линию можно рассматривать как траекторию движения точки в пространстве или совокупность точек , удовлетворяющих определенному уравнению. Кривые линии подразделяются на плоские и пространственные, на алгебраические, трансцендентные и эмпирические, монотонные и составные ( рис.1.7 ).

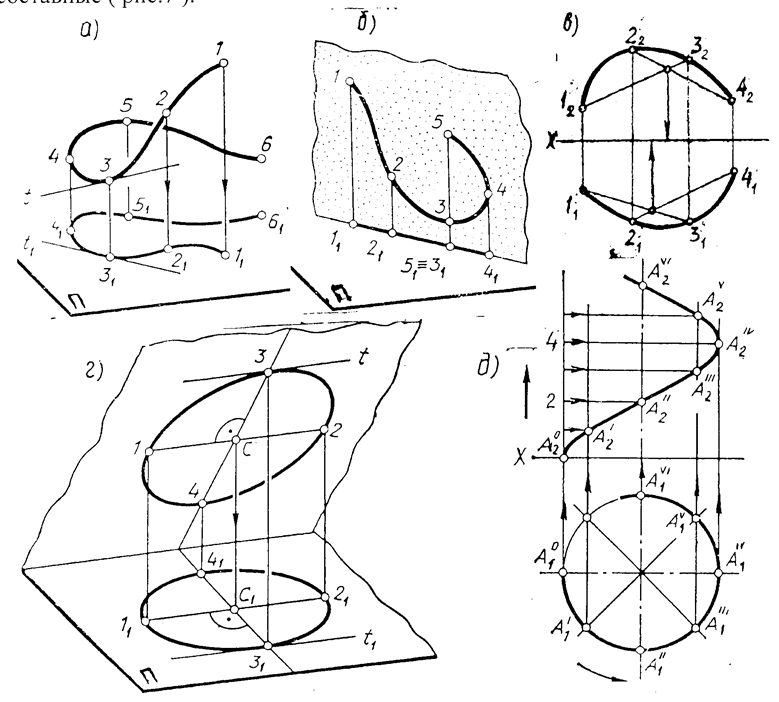
Рис 1.7.  Изображения кривых линий: а, в – пространственных, б, г – плоских,

д – винтовой линии.

      Для построения ортогональных проекций кривой нужно построить проекции ряда точек, принадлежащих этой кривой и соединить между собой одноименные проекции в той последовательности, в какой они находятся в оригинале. Чтобы решить по эпюру, какая кривая в натуре ( плоская или пространственная ), нужно произвольно провести две хорды. Если хорды пересекаются – кривая плоская,  если скрещиваются – пространственная ( см. рис.1.7в ). Классическим примером плоской кривой является окружность, которая может проецироваться на плоскость в линию, в окружность и в общем случае в виде эллипса ( см. рис.1.7г ). При проецировании окружности любая пара ее взаимно перпендикулярных диаметров проецируется парой сопряженных диаметров эллипса. Диаметр (1-2) окружности, параллельной плоскости П  проецируется без искажения и является для эллипса – проекции большой осью (1₁-2₁). Примером пространственной кривой является винтовая линия ( см. рис.1.7д ).

1.5.  Ортогональные  проекции поверхностей

       Под поверхностью подразумевается непрерывное множество точек. Поверхности так же могут быть алгебраическими и трансцендентными.

Множество точек или линий, определяющих поверхность, называется ее каркасом.

     1.5.1. В начертательной геометрии поверхность рассматривается как совокупность всех последовательных положений некоторой линии, называемой образующей, перемещающейся в пространстве по определенному закону. Закон образования поверхности графически задается в виде линий образующих (l) и направляющих (m) .Этот способ образования поверхности называется кинематическим, а элементы поверхности – определителем.

    1.5.2. Чтобы задать поверхность на чертеже, достаточно указать проекции ее определителя – образующих и направляющих (рис.1.8а ). В ряде случаев поверхность удобно задавать ее очерком – следом на плоскости проекций огибающей цилиндрической поверхности, а для поверхности вращения – осью вращения, проекциями экватора и главного меридиана ( рис.1.8б ).

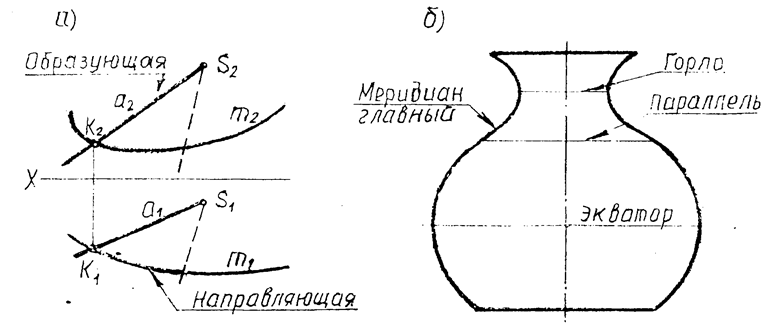
Рис  1.8.  Изображения поверхности кинематическим способом и очерком поверхности вращения.

     1.5.3.  Многообразие форм поверхностей создает большие трудности при их анализе. В основу их систематизации может быть положено единство способа их образования – определитель: Ф (Г) [A].

Геометрическая часть (Г) включает образующие – прямые (ā) и кривые (ã) линии. Криволинейные образующие могут быть постоянного и переменного вида. По этому признаку поверхности подразделяются на линейчатые и нелинейчатые. Первые могут иметь одну, две, три направляющие (m), которые также могут быть прямыми и кривыми линиями.

    Алгоритмическая часть определителя [A] может содержать закон перемещения образующей и закон изменения формы образующей [ A₁ ]. По этим признакам поверхности можно разделить на классы, подклассы, группы, виды. Некоторые из указанных поверхностей приведены в табл.1.5.

Таблица.1.5.

Поверхности