Проецирование геометрических фигур, страница 3

      1.3.2. Прямая линия определяется двумя точками, поэтому прямая считается заданной,  если на эпюре даны проекции двух ее точек, включая ее следы – точки пересечения плоскостей проекций. Две проекции прямой определяют положение прямой в пространстве. Проекция прямой – в общем случае – прямая линия. Прямые могут занимать различные положения по отношению к плоскостям проекций. Прямая общего положения – это прямая наклоненная к  П₁, П₂, П₃ ( рис.1.4 ).

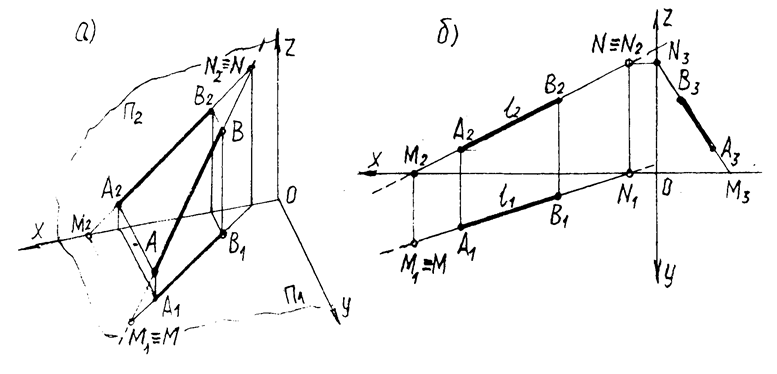
Рис 1.4.  Изображения прямой общего положения.

Прямые частного положения подразделяются на прямые уровня  (параллельные П ) и проецирующие ( перпендикулярные П ). Характерные особенности этих прямых и их проекций в первом октанте приведены в табл.1.3.

Таблица 1.3

   Прямые  частного  положения.

1.3.3.  Плоскость определяется тремя точками, не лежащими на одной прямой; прямой и точкой, не принадлежащей прямой; двумя пересекающимися прямыми; двумя параллельными прямыми; плоской фигурой (рис.1.5а,б,в,г), а также следами. След плоскости – это линия пересечения плоскости с плоскостями проекций. В общем случае плоскость может иметь три следа:  горизонтальный h₀, фронтальный f₀, профильный p₀ . Треугольник Σx Σy Σz называется треугольником следов  ( рис.1.5д ). Треугольник следов может быть замкнут в I октанте (рис.1.5д) или в IV октанте (см.рис.1.5е). При этом следы f₀и h₀могут совпадать , если плоскость равнонаклонена к П₁ и П₂. 

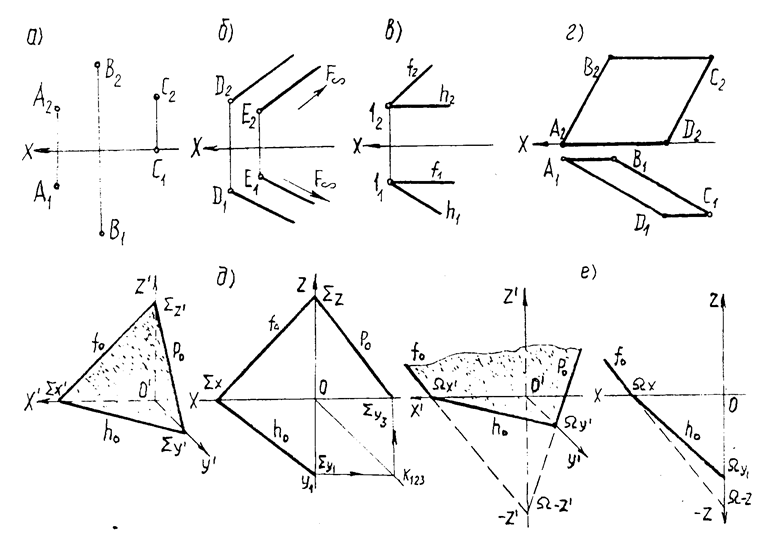
                                            Рис 1.5.  Изображения плоскости.

      Плоскости относительно плоскостей проекций также занимают различные положения: плоскости общего положения наклонены ко всем плоскостям проекций ( см.рис.1.5 ) ; плоскости уровня – параллельны плоскостям проекций; плоскости проецирующие – перпендикулярны плоскостям проекций. Характерные особенности плоскостей частного положения приведены в табл.1.4.  

Таблица 1.4

 Плоскости  частного  положения

      1.3.4.  Многогранники представляют собой тела, ограниченные несколькими плоскостями т.е. гранями. Изображение многогранников сводится к изображению ребер ( линий пересечения граней ) и вершин ( точек пересечения ребер ).  Простейший многогранник – четырехгранник – изображается четырьмя вершинами и шестью ребрами. Построение других многогранников (пирамид и призм) подобно четырехграннику ( рис.1.6 ).

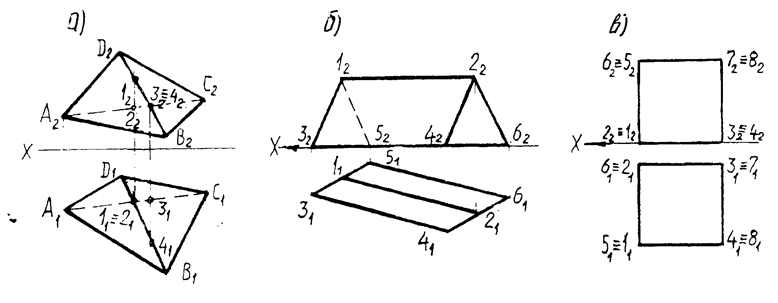
Рис 1.6.  Изображения многогранников на эпюре: а – пирамиды, б – призмы,

г – гексаэдра (куба).

      Известны пять правильных многогранников ( платоновы тела ), гранями которых являются правильные многоугольники. Тетраэдр – 4 грани – равносторонние треугольники; гексаэдр ( куб ) – 6 граней – квадратов; октаэдр – 8 граней – равносторонних треугольников; додекаэдр – 12 граней – пятиугольников ( пентагонов ); икосаэдр – 20 граней – правильных треугольников.Для любого выпуклого многогранника число вершин (В), ребер (Р) и граней (Г) связаны формулой Эйлера: В – Р + Г = 2.

     Если грани многогранника перпендикулярны какой-либо плоскости, то он занимает по отношению к ней частное положение ( см.рис.1.6в ). При построении многогранников нужно устанавливать видимость ребер методом конкурирующих точек: на плоскости П₁ будет видна одна из двух точек   (1,2) проецирующей прямой, у которой координата Z больше ( Z₁ > Z₂ ); на плоскости  П₂ - та , у которой координата Y больше ( Y₄ > Y₃ ). Следовательно будут видны  те ребра, точки которых видны ( см. рис.1.6а ).