Проецирование геометрических фигур, страница 2

                ( C Є [AB]  ^   ). 

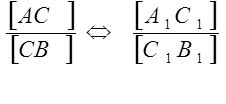1.2.  Виды проекций

     1.2.1. Наиболее полно требованиям к чертежам ( наглядность, обратимость, простота, точность ) отвечают ортогональные проекции, которые явились основой для создания в 1798 году французским математиком Г.Монжем систематизированного учебника по начертательной геометрии. Метод Монжа предусматривает получение изображений на две-три взаимно перпендикулярные плоскости ( рис.1.3а ): П₁ - горизонтальная плоскость, П₂ - фронтальная и П₃ – профильная плоскости с последующим их совмещением в одну плоскость (рис.3б). Соответственно А₁, A₂, A₃ – горизонтальная, фронтальная и профильная проекции точки. Для чтения эпюра необходимо мысленно свернуть плоскости в пространственную систему Оxyz и восстановить проецирующие лучи в пространстве.

      1.2.2. Косоугольное параллельное проецирование положено в основу метода аксонометрических проекций, сущность которого заключается в том ,  что объект проецируется на единственную плоскость П' вместе с некоторой системой координат ( рис.1.3в ).

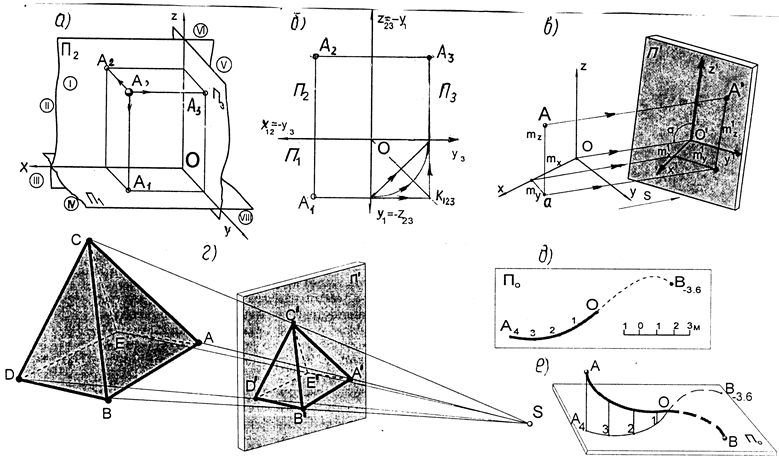
      Рис 1.3.  Виды проекций: а, б – прямоугольные; в – аксонометрические,

г – перспективные; д, е – с числовыми отметками.

      Ортогональные и аксонометрические проекции являются основными при проектировании большинства изделий. При проектировании строительных объектов дополнительно применяются проекции с числовыми отметками и перспективные проекции.

      1.2.3. Перспективные проекции основаны на применении центрального проецирования и представляют собой изображение объектов на картинную плоскость ( рис.1.3г ). Перспективы отличаются хорошей наглядностью, т.к. соответствуют тем кажущимся изменениям величин и очертаний объектов, которые обусловлены их удаленностью от точки наблюдения и их положением в пространстве. Однако они трудоемки в исполнении и плохо измеримы.

     1.2.4. В проекциях с числовыми отметками строительный объект ( полотно железной или шоссейной дороги, аэродромы, площадки и т.п.  ) проецируются ортогонально только на одну плоскость нулевого уровня. Высота точек объекта от этой плоскости указывается отметками – числами в виде индексов к обозначениям проекций. Такие чертежи называются планами ( рис.1.3д,е  ).

1.3.   Ортогональные проекции точки, прямой,

 плоскости, многогранников

      1.3.1. Две плоскости делят пространство на 4, а три плоскости – на 8 октантов ( см. рис.1.3а ). Чтобы определить положение точки в любом октанте, устанавливают знаки координат. Координаты точки – это расстояния от точки до плоскостей проекций. Точка в пространстве определяется тремя координатами, каждая из ( трех ) проекций точки определяется двумя координатами:  А(x,y.z), A₁(x,y), A₂(x,z), A₃(y,z). Координаты точки могут быть равными нулю и отрицательными. Тогда точка может лежать на плоскости проекций или находиться в любом из 8 октантов. Значения координат и эпюры точек при различных  положениях точки даны в табл.1.1 и табл.1.2. Две проекции точки вполне определяют положение точки в пространстве.

                                             Таблица 1.1                                                                              

Точка  в  октантах  II…VIII                 

                                                Таблица 1.2

Точка  в  плоскости  и  на  оси