








Законы сохранения следуют из уравнений движения и в определенных условиях практически эквивалентны им. Однако в ряде случаев законы сохранения предоставляют возможность сделать весьма полные выводы о характере движения без необходимости непосредственного решения соответствующих уравнений движения.
С некоторыми из законов сохранения мы уже знакомы. Это закон сохранения массы, математическим выражением которого является уравнение неразрывности, и закон сохранения импульса, следующий из второго закона Ньютона. Закон сохранения энергии находит отражение в уравнении Бернулли, а закон сохранения момента импульса - в теореме Кельвина или в теореме Эртеля в зависимости от совокупности ограничений, накладываемых на процесс движения. В формулировке теоремы Эртеля используется новая физическая величина – потенциальный вихрь. В последние десятилетия существенный прогресс в понимании динамики атмосферы связан с использованием для анализа движения особенностей изменения именно этой величины.
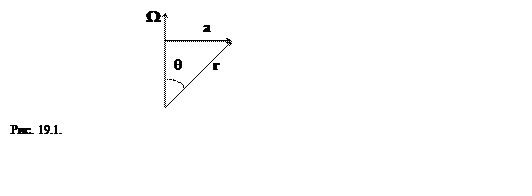 |
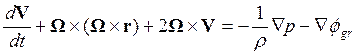 , (19.1)
, (19.1)
где
V –
вектор относительной скорости
(скорость по отношению к выбранной горизонтальной системе координат, жестко
связанной с вращающейся Землей и c началом
координат на поверхности Земли), ![]() - вектор угловой
скорости вращения Земли,
- вектор угловой
скорости вращения Земли, ![]() - потенциал силы
тяжести (гравитационный потенциал). В частности, если g
– вектор, противоположный силе тяжести и равный по величине ускорению
свободного падения, то
- потенциал силы
тяжести (гравитационный потенциал). В частности, если g
– вектор, противоположный силе тяжести и равный по величине ускорению
свободного падения, то ![]() , где вектор r–
радиус-вектор точки. Убедитесь сами, что градиент такого потенциала со знаком
минус приводит к правильному значению силы гравитации, действующей на единицу
массы: -g. Три члена в левой части уравнения (19.1) имеют смысл
относительного ускорения, центростремительного ускорения и ускорения Кориолиса
соответственно. Мы постараемся по возможности выразить эти члены в виде
градиента скалярных функций.
, где вектор r–
радиус-вектор точки. Убедитесь сами, что градиент такого потенциала со знаком
минус приводит к правильному значению силы гравитации, действующей на единицу
массы: -g. Три члена в левой части уравнения (19.1) имеют смысл
относительного ускорения, центростремительного ускорения и ускорения Кориолиса
соответственно. Мы постараемся по возможности выразить эти члены в виде
градиента скалярных функций.
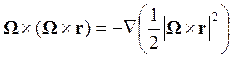 .
.
Вектор ![]() перпендикулярен
плоскости, в которой лежат векторы
перпендикулярен
плоскости, в которой лежат векторы ![]() и
и ![]() , и равен по величине произведению
, и равен по величине произведению ![]() , где
, где ![]() ,
, ![]() - угол между векторами
- угол между векторами ![]() и
и ![]() (см.
рис. 19.1). Тогда, если вектор угловой скорости умножить на перпендикулярный
ему вектор
(см.
рис. 19.1). Тогда, если вектор угловой скорости умножить на перпендикулярный
ему вектор ![]() , результат будет иметь длину
, результат будет иметь длину ![]() и направление, противоположное вектору а.
и направление, противоположное вектору а.
Выражение под знаком градиента равно ![]() . Равенство, которое мы хотим доказать,
должно быть справедливо в любой системе координат. Направим ось z вдоль вектора
угловой скорости
. Равенство, которое мы хотим доказать,
должно быть справедливо в любой системе координат. Направим ось z вдоль вектора
угловой скорости ![]() . Тогда получим
. Тогда получим 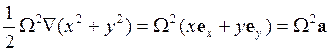 , что доказывает равенство. Обратите
внимание также на то, что вектор
, что доказывает равенство. Обратите
внимание также на то, что вектор ![]() есть ни что иное, как
вектор линейной скорости вращения неподвижной в горизонтальной системе координат
точки вокруг оси
есть ни что иное, как
вектор линейной скорости вращения неподвижной в горизонтальной системе координат
точки вокруг оси ![]() . Следовательно, под знаком
градиента в правой части доказанного равенства стоит кинетическая энергия
вращения покоящейся в горизонтальной системе координат единицы массы жидкости
вокруг оси
. Следовательно, под знаком
градиента в правой части доказанного равенства стоит кинетическая энергия
вращения покоящейся в горизонтальной системе координат единицы массы жидкости
вокруг оси ![]() . Полученное выражение для
центростремительного ускорения, будучи перенесенным в правую часть уравнения
движения, может быть объединено с гравитационным потенциалом
. Полученное выражение для
центростремительного ускорения, будучи перенесенным в правую часть уравнения
движения, может быть объединено с гравитационным потенциалом ![]() для формирования геопотенциала
для формирования геопотенциала 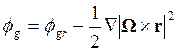 (работы, затрачиваемой на поднятие
единицы массы на заданную высоту).
(работы, затрачиваемой на поднятие
единицы массы на заданную высоту).
Две проекции ускорения из (19.1), относящиеся к горизонтальному движению, превалируют над третьей, относящейся к вертикальному движению, и определяют условия баланса ускорения Кориолиса и градиента давления.
Полная производная по времени по смыслу связана с
движущейся частицей жидкости. В эйлеровых координатах выражение для полной
производной имеет вид 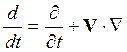 (см. разд. 14.3).
Возникающий в связи с этим в уравнении движения нелинейный адвективный член
(см. разд. 14.3).
Возникающий в связи с этим в уравнении движения нелинейный адвективный член ![]() можно представить в виде
можно представить в виде
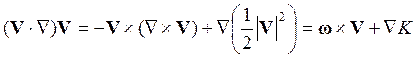 ,
,
где
символом K обозначена кинетическая энергия единицы массы
жидкости, а ![]() - называется вектором относительного
вихря[1].
Этот вектор определяет скорость и направление вращения воздуха в заданной точке
пространства. Мы уже знаем, что воздух, вращаясь, перемещается из областей
высокого давления в области с низким давлением, и горизонтальные компоненты
вектора скорости значительно превышают вертикальную. Следовательно, вектор
относительного вихря имеет преимущественно вертикальную компоненту. Если происходит
вращение против часовой стрелки (циклоническое), как это происходит вокруг
области низкого давления, вертикальная компонента относительного вихря
положительна. В случае антициклонического вращения – отрицательна.
- называется вектором относительного
вихря[1].
Этот вектор определяет скорость и направление вращения воздуха в заданной точке
пространства. Мы уже знаем, что воздух, вращаясь, перемещается из областей
высокого давления в области с низким давлением, и горизонтальные компоненты
вектора скорости значительно превышают вертикальную. Следовательно, вектор
относительного вихря имеет преимущественно вертикальную компоненту. Если происходит
вращение против часовой стрелки (циклоническое), как это происходит вокруг
области низкого давления, вертикальная компонента относительного вихря
положительна. В случае антициклонического вращения – отрицательна.
С учетом полученных соотношений находим из (19.1) для локальной производной от скорости
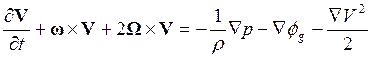 . (19.2)
. (19.2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.