Законы сохранения. Уравнение Бернулли. Абсолютный и потенциальный вихри. Теорема Эртеля, страница 2

Рассмотрим теперь случай стационарного течения несжимаемой жидкости. Под стационарным понимается поток, скорость которого в любой точке не меняется во времени. Таким образом, картина скоростей всегда выглядит одинаково во все моменты времени, и, следовательно, линии тока остаются также неизменными во времени. Следует  иметь в виду, что стационарность вовсе не означает, что частички жидкости движутся с постоянными скоростями: переходя от точки к точке вдоль линии тока они могут менять свою скорость. Просто в каждой точке пространства скорость не меняется во времени, и .

Умножим уравнение (19.2) скалярно на скорость. Тогда с учетом сказанного и в приближении постоянства плотности жидкости имеем

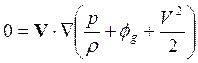                                       ,                                                      (19.3)

где учтено, что векторы перпендикулярны вектору скорости. Согласно полученному результату, при движении градиент выражения внутри скобок перпендикулярен вектору скорости - то есть, как уже обсуждалось, линии тока. Иными словами, составляющая градиента вдоль линии тока равна нулю. Но это означает, что в стационарном потоке несжимаемой невязкой жидкости выражение в скобках не меняется вдоль линии тока:

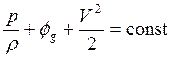                                                         .                                                  (19.4)

Выражение (19.4) называется теоремой Бернулли[2]. В общем случае константа в (19.4) может быть разной для разных линий тока. Однако, если рассматриваемый стационарный поток является  безвихревым ( во всех точках пространства), то из уравнения (19.2) следует, что

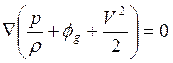                                                            ,                                                (19.3΄)

то есть, теперь постоянная в (19.4) – одна и та же для всей жидкости.

Как отмечалось выше, теорема Бернулли не означает ничего большего, чем закон сохранения энергии: сумма работы сил давления, потенциальной энергии и  кинетической энергии относительного движения единицы массы жидкости постоянна вдоль линии тока (или во всей жидкости в случае безвихревого движения)[3].

Выше предполагалось, что в процессе движения плотность жидкости не меняется. Если такое допущение неприемлемо, можно элементарно показать, что сохраняющейся величиной вдоль линии тока будет сумма левой части (19.4) с внутренней энергией единицы массы жидкости. Внутренняя энергия может соответствовать тепловой энергии сжимаемой жидкости или химической энергии, которые могут изменяться от точки к точке вдоль линии тока.

19.2. Абсолютный и потенциальный вихри. Теорема Эртеля

Если взять операцию ротора от левой и правой частей уравнения (19.2), то все члены в виде градиента различных функций обратятся в ноль, так как для любой функции  [4], и  уравнение примет вид

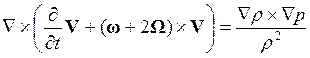                                          .                            (19.5)

Вектор 

                                                                                                                         (19.6)            

называют вектором абсолютного  вихря[5], а вектор в правой части уравнения (19.5) - бароклинным. Этот вектор определяет степень наклона поверхностей постоянного давления к поверхностям постоянной плотности[6]. Когда эти поверхности параллельны,  или  жидкость несжимаема[7], бароклинный вектор равен нулю, и жидкость называют баротропной. Однако такая ситуация бывает далеко не всегда.

В левой части уравнения поменяем местами операции дифференцирования по времени и по координатам и внесем под знак производной по времени постоянный вектор :

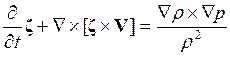                                         .                                               (19.7)

Умножим теперь обе части уравнения скалярно на градиент функции, которая зависит только от давления и плотности . Нетрудно, видеть, что такой градиент 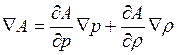 всегда перпендикулярен бароклинному вектору (поскольку  лежит в плоскости векторов  и , а бароклинный вектор перпендикулярен им), и правая часть уравнения исчезает: