Потенциальный вихрь – скалярная величина, поэтому задача определения потенциального вихря оказывается более простой с математической точки зрения, чем задача решения уравнений движения для вектора скорости. Определив потенциальный вихрь, можно найти и вектор скорости движения подобно тому, как мы находим вектор напряженности электрического поля, зная распределение скалярного электрического потенциала.
В большинстве приложений к динамике атмосферы в
качестве скалярной величины, используемой для определения потенциального
вихря, выбирается потенциальная температура ![]() , которая
непосредственно связана с энтропией
, которая
непосредственно связана с энтропией ![]() соотношением
соотношением ![]() , где
, где ![]() -
теплоемкость при постоянном давлении (см. разд. 13). Следовательно, если
постоянна потенциальная температура, постоянна и энтропия. А постоянство
энтропии означает, что мы имеем дело с адиабатическим процессом. Таким образом,
если в процессе движения потенциальная температура частицы воздуха или жидкости
не меняется, изменение состояния частицы в ходе движения происходит
адиабатически, и энтропия частицы тоже не меняется. Следовательно движение
частицы происходит по изэнтропической поверхности - поверхности, на
которой энтропия постоянна.
-
теплоемкость при постоянном давлении (см. разд. 13). Следовательно, если
постоянна потенциальная температура, постоянна и энтропия. А постоянство
энтропии означает, что мы имеем дело с адиабатическим процессом. Таким образом,
если в процессе движения потенциальная температура частицы воздуха или жидкости
не меняется, изменение состояния частицы в ходе движения происходит
адиабатически, и энтропия частицы тоже не меняется. Следовательно движение
частицы происходит по изэнтропической поверхности - поверхности, на
которой энтропия постоянна.
Удобство использования потенциальной температуры, заключается также в том, что поскольку плотность воздуха с высотой уменьшается экспоненциально, утверждение «горячий воздух поднимается вверх» не совсем корректно. Ведь горячий воздух внизу при поднятии может оказаться более плотным, чем холодный воздух вверху, а, следовательно, подниматься перестанет. Но это утверждение абсолютно верно, когда речь идет о потенциальной температуре воздуха.
Крупномасштабные движения атмосферы происходят в
горизонтальном направлении, следовательно, вертикальная компонента вектора
абсолютного вихря будет доминировать над горизонтальной. Здесь имеется в виду
местное направление, противоположное силе тяжести. Введем единичный вектор
местной вертикали ![]() и обозначим
и обозначим
![]() ,
,
где
![]() - географическая широта. Таким образом,
величина
- географическая широта. Таким образом,
величина ![]() есть ранее введенный параметр Кориолиса,
который растет по мере увеличения широты. Тогда с учетом принятого выбора
величины А получаем
есть ранее введенный параметр Кориолиса,
который растет по мере увеличения широты. Тогда с учетом принятого выбора
величины А получаем
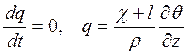 .
(19.13)
.
(19.13)
Поскольку вертикальные ускорения можно считать малыми для крупномасштабных, преимущественно горизонтальных движений, мы используем гидростатическое приближение, согласно которому левая часть уравнения движения для вертикальной компоненты пренебрежимо мала:
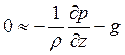 .
.
Далее, для земной атмосферы с хорошей точностью можно считать, что ускорение силы тяжести постоянно. Тогда выражение (19.13) можно переписать в виде
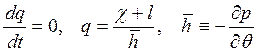 ,
(19.14)
,
(19.14)
где
мы переопределили величину q, введя в нее константу g. Переменная ![]() является положительно определенной в
случае устойчивой стратификации атмосферы и играет роль высоты вихревой трубки,
упоминавшейся ранее.
является положительно определенной в
случае устойчивой стратификации атмосферы и играет роль высоты вихревой трубки,
упоминавшейся ранее.
Величину, обратную ![]() ,
называют статической устойчивостью. Действительно, чем быстрее растет
потенциальная температура по мере уменьшения давления при увеличении высоты,
тем устойчивее стратификация атмосферы. В этом отношении стратосфера
характеризуется особенно высокой статической устойчивостью. Наоборот, если
величина
,
называют статической устойчивостью. Действительно, чем быстрее растет
потенциальная температура по мере уменьшения давления при увеличении высоты,
тем устойчивее стратификация атмосферы. В этом отношении стратосфера
характеризуется особенно высокой статической устойчивостью. Наоборот, если
величина ![]() близка к нулю или становится
отрицательной, стратификация атмосферы становится, очевидно, весьма неустойчивой
(см. также разд. 13.5).
близка к нулю или становится
отрицательной, стратификация атмосферы становится, очевидно, весьма неустойчивой
(см. также разд. 13.5).
Согласно (19.14), при движении по изэнтропической поверхности сохраняется произведение величины абсолютного вихря и статической стабильности. Если один из сомножителей изменяется, то второй сомножитель изменяется в противоположном направлении, чтобы произведение осталось постоянным.
Следует сказать несколько слов о происхождении
названия потенциальный вихрь. Здесь слово потенциальный играет ту же
роль, что и для термина потенциальная температура. Фактически потенциальный
вихрь определяет значение относительного вихря ![]() , которым
обладала бы частица воздуха будучи перемещенной на некоторую стандартную широту
при стандартном значении статической устойчивости.
, которым
обладала бы частица воздуха будучи перемещенной на некоторую стандартную широту
при стандартном значении статической устойчивости.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.