Циклоны и антициклоны представляют собой воздушные вихри большого масштаба. Поэтому качественные выводы об условиях возникновения и движения циклонов и антициклонов тоже можно сделать на основе уравнения переноса потенциального вихря [17].
В заключение рассмотрим влияние
вязкости на эволюцию абсолютного вихря в случае несжимаемой жидкости. В
этом случае в уравнении движения появляется справа дополнительный член 
, где 
-
коэффициент кинематической вязкости (разд. 14.4). Операторы ротора и Лапласа
можно поменять местами, тогда учет вязкости и несжимаемости (
) приведет к появлению в уравнении для
абсолютного вихря дополнительного члена:
.
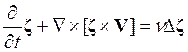Показать, что при определенных условиях поле скоростей однозначно определяется полем скалярного потенциального вихря.
Объяснить природу волн Россби на языке потенциального вихря.
[1] Фактически это есть удвоенная мгновенная угловая скорость частицы жидкости в выбранной нами системе координат. Действительно, пусть частица, положение которой определяется радиус-вектором , вращается вокруг оси с угловой скоростью (рис. 19.1). Линейная скорость движения частицы вокруг оси есть . Для простоты направим ось z системы координат вдоль вектора угловой скорости. Тогда . Ротор от этого выражения есть .
Справедливость выражения для адвекции вектора скорости проще всего показать, выписывая декартовы компоненты векторов в левой и правой частях равенства.
[2] D. Bernoulli (1700-1782) – младший представитель семьи швейцарских ученых, иностранный почетный член Пербургской академии наук (1733).
[3] При выводе теоремы Бернулли использовалось предположение о стационарности течения. Очевидно, что условие стационарности зависит от выбора системы координат, в которой рассматривается течение. В частности, в системе координат, в которой жидкость покоится на бесконечности, ламинарное течение, возникающее от медленно движущегося в жидкости тела, не будет стационарным даже при постоянной скорости движения тела. Однако в системе координат, связанной с телом, течение будет стационарным.
Выбор системы координат сказывается также на величине потенциальной энергии. В частности, в случае системы координат, вращающейся вместе с Землей, потенциальная энергия включает в себя также и член, обусловленный центростремительным ускорением (то есть, кинетическую энергию вращательного переносного движения).
[4] Действительно, , поскольку определитель с двумя одинаковыми строками всегда равен нулю.
[5] Вектор абсолютного вихря определяет удвоенную мгновенную угловую скорость частицы в исходной инерциальной системе координат. Согласно (19.6), он равен сумме векторов относительного и планетарного (2Ω) вихрей.
[6] Действительно, оба градиента перпендикулярны соответствующим поверхностям, следовательно, их векторное произведение пропорционально синусу угла между поверхностями.
[7] В случае несжимаемой жидкости любая поверхность (в том числе и поверхность постоянного давления) является одновременно и поверхностью постоянной плотности.
[8] Сохраняющаяся масса фигуриста играет в этом случае роль «энтропии».
[9] Чтобы доказать это равенство, нужно выписать компоненты ротора вектора скорости и применить к ним операцию дивергенции.
[10] . Здесь второй член равен нулю, поскольку величина A сохраняется. Производную по времени от плотности заменяем с учетом уравнения неразрывности и получаем выражение (19.12).
[11] Единицы измерения потенциального вихря. Потенциальный вихрь выражают в единицах . Обычно стратосферному воздуху соответствуют значения выше 1.5 – 2 PVU, тропосферному – меньшие.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.