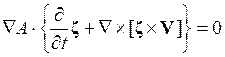 .
(19.8)
.
(19.8)
Нашей окончательной целью является представить
выражение (19.8) в виде полной производной по времени: ![]() и
таким образом получить закон сохранения потенциального вихря. Чтобы
прийти к нему, величина А сама по себе должна быть сохраняющейся
величиной:
и
таким образом получить закон сохранения потенциального вихря. Чтобы
прийти к нему, величина А сама по себе должна быть сохраняющейся
величиной: ![]() . Обычно в качестве такой величины
используют энтропию. Тогда значение энтропии будет выступать в качестве одного
из «маркеров», выделяющих частицу жидкости или воздуха из других, если энтропия
частицы в ходе движения не изменяется. Градиент величины А будет определять
масштаб для измерения «расстояния» между различными частицами (будет служить
мерой различия), и будет использоваться для измерения длины вихревых трубок.
. Обычно в качестве такой величины
используют энтропию. Тогда значение энтропии будет выступать в качестве одного
из «маркеров», выделяющих частицу жидкости или воздуха из других, если энтропия
частицы в ходе движения не изменяется. Градиент величины А будет определять
масштаб для измерения «расстояния» между различными частицами (будет служить
мерой различия), и будет использоваться для измерения длины вихревых трубок.
Простейший пример вихревой трубки – это столб воды, вращающийся внутри некоторого большего объема воды. Если сечение столба уменьшается, его длина должна возрасти, ради сохранения массы. Но при уменьшении сечения следует также ожидать, что скорость вращения жидкости возрастет, чтобы сохранить угловой момент. Это подобно тому, как фигурист увеличивает скорость вращения, прижимая руки плотно к телу[8]. Таким образом, длина трубки и ее угловая скорость коррелируют, а их сохраняющееся отношение как раз и есть потенциальный вихрь.
Закон сохранения потенциального вихря впервые был сформулирован Эртелем (H. Ertel) в 1942 году в Германии. Согласно этому закону,
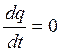 ,
(19.9)
,
(19.9)
где
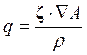 .
(19.10)
.
(19.10)
Здесь величина qи есть потенциальный вихрь. Он получается посредством взятия производной от Aпо направлению абсолютного вихря и последующего деления на плотность.
Чтобы прийти от (19.8) к окончательному результату (19.9), воспользуемся сначала векторным равенством
![]() ,
,
где скобки определяют последовательность операций (сначала выполняется операция в скобках). Равенство может быть доказано непосредственным вычислением декартовых компонент векторов в левой и правой частях. С его использованием выражение (19.8) можно переписать в виде
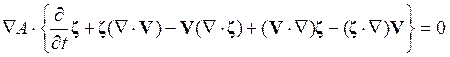 . (19.11)
. (19.11)
Третий
член в скобках равен нулю, поскольку ![]() [9].
Последний член сам по себе может быть отличен от нуля, однако скалярное
произведение с градиентом А всегда равно нулю. Действительно, вектор
[9].
Последний член сам по себе может быть отличен от нуля, однако скалярное
произведение с градиентом А всегда равно нулю. Действительно, вектор ![]() перпендикулярен поверхности
перпендикулярен поверхности ![]() , по которой происходит движение, поскольку
мы предположили, что величина А сохраняется в ходе движения. В то же
время вектор скорости касается этой поверхности. Легко убедиться, что
скалярный дифференциальный оператор не может нарушить это соотношение. Для
доказательства выберем систему координат с осью z параллельной
градиенту
, по которой происходит движение, поскольку
мы предположили, что величина А сохраняется в ходе движения. В то же
время вектор скорости касается этой поверхности. Легко убедиться, что
скалярный дифференциальный оператор не может нарушить это соотношение. Для
доказательства выберем систему координат с осью z параллельной
градиенту ![]() . Тогда вектор скорости имеет только x
и y компоненты, и никакие скалярные операторы, действующие на этот
вектор, не могут привести к появлению z-компоненты. Следовательно,
скалярное произведение сохранит свое нулевое значение.
. Тогда вектор скорости имеет только x
и y компоненты, и никакие скалярные операторы, действующие на этот
вектор, не могут привести к появлению z-компоненты. Следовательно,
скалярное произведение сохранит свое нулевое значение.
Для полной производной по времени от потенциального
вихря (19.10) с учетом постоянства величины А и уравнения неразрывности
- ![]() - получаем[10]
- получаем[10]
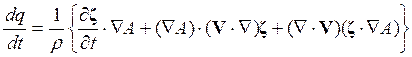 , (19.12)
, (19.12)
что
с учетом проведенного обсуждения с точностью до множителя ![]() совпадает с (19.11). Следовательно, равенство
(19.9) доказано.
совпадает с (19.11). Следовательно, равенство
(19.9) доказано.
Три условия должны выполняться, чтобы потенциальный вихрь сохранялся при движении:
1. движение происходит без трения;
2. величина A является константой движения (сохранятся сама по себе);
3. жидкость баротропна или величина Aесть функция только давления и плотности.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.