Ионосфера. Ионизация. Соотношение между концентрацией свободных электронов и отрицательных ионов. Отражение радиоволн от ионосферы, страница 12

d²x/dt²=-k²x²+r sinωt.

Здесь параметр k характеризует упругие силы, препятствующие смещению частицы. Численно он равен частоте собственных колебаний частицы в отсутствие внешних воздействий. Чем больше значение параметра, тем ближе мы к случаю диэлектрика (сильно связанных зарядов). Параметр r характеризует величину отнесенной к единице массы частицы внешней силы, вызывающей ее смещение.

         Будем искать решение в виде x=asinωt, предполагая, что собственные свободные колебания осциллятора неактивны (то есть, не возбуждены). Подстановка в уравнение движения дает

                                           -aω² sinωt=-k²asinωt,

или

a(k²-w²)=r,   a=r/( k²-w²).

Таким образом,

1) при ω< k фазы движения и возбуждающей силы совпадают (знаки а и r совпадают – случай диэлектрика);

2) при ω> k фазы противоположны (случай свободных зарядов);

3) при ω≈k наступает резонанс и амплитуда устремляется в бесконечность.

Здесь следует обратить внимание на одно важное обстоятельство. Решая дифференциальное уравнение, мы предположили, что сила действует бесконечно долго. Действительно, данное решение справедливо и при ,  а не только при t>0.

         Получить решение задачи, когда до момента t=0 система покоилась, а затем появилась внешняя сила, и началось движение, значительно труднее. Однако ясно, что при больших значениях t такое решение начнет совпадать с уже полученным. В частности, в условиях резонанса амплитуда колебаний, равная нулю при t=0,   постепенно начинает расти до бесконечности при . Иными словами, в условиях резонанса осциллятор все время накапливает энергию, подтверждением чему является все возрастающая амплитуда колебаний.

Рассмотрим теперь случай, когда действует сила трения. Природа этой силы не имеет существенного значения. Важно, что во всех случаях трение обязано взаимодействию нашей частицы с другими объектами. В результате такого взаимодействия энергия движения частицы передается объекту, с которым она взаимодействует. В самом грубом приближении можно считать, что величина силы трения пропорциональна скорости движения частицы. Поэтому уравнение движения принимает вид

d²x/dt²=-k²x-qdx/dt+rsinωt,

где qdx/dt - сила трения, отнесенная к единице массы частицы, причем, очевидно, (сила трения препятствует росту величины ускорения). Будем искать решение в виде x=a sinωt+b cosωt. При таком выборе мы допускаем произвольное смещение фазы колебаний относительно фазы вынуждающей силы. Подставляем общий вид решения в уравнение движения:

-aω²sinωt – bω²cosωt=-ak²sinωt-bk²cosωt+aωqcosωt-bωqsinωt+r sinωt.

Равенство должно выполняться при любых значениях t. Пусть t=0. Тогда

                              (k²-ω²)b=aωqилиb=aωq/(k²-ω²).

Пусть t=π/2ω. Тогда

                                      (k²-ω²)a=-qbω+r.

Из полученных двух уравнений находим

,

                                 .

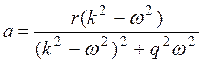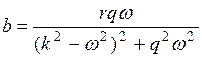Таким образом,

1) при , то есть, фазы возмущающей силы (напряженности поля) и движения совпадают;

2) при  и фазы противоположны;

3) наконец, при  имеем случай резонанса: , и фаза сдвинута на 90˚.

         В случае наличия трения амплитуда колебаний при резонансе не бесконечна: чем больше трение (взаимодействие) q, тем меньше амплитуда установившихся колебаний[10]. Таким образом, характер движения существенно зависит от соотношения между частотой собственных колебаний осциллятора и частотой внешней силы.  Если последняя значительно превышает первую, получаем модель, характерную для несвязанных (свободных) зарядов – плазмы. Если наоборот, - имеем случай диэлектрика, где заряды существенно несвободны.