Ионосфера. Ионизация. Соотношение между концентрацией свободных электронов и отрицательных ионов. Отражение радиоволн от ионосферы, страница 10

В электрическом разряде в газе внешний источник электроэнергии передает энергию непосредственно электронам (носителям тока), а ионы и нейтральные частицы приобретают энергию благодаря столкновениям с быстрыми электронами. Нечто подобное происходит и в ионосфере. В частности, в области F температура электронов днем в 1.5-2 раза выше температуры нейтральных частиц и может достигать 3000 ⁰С.  Ночью разница  температур уменьшается до нескольких сот градусов. В самой низкой области ионосферы (D), где плотность частиц велика, электронная температура  практически не отличается от температуры нейтралов.

Существенно, что очень малая доля энергии передается при столкновении от электрона иону из-за разницы в массах. Элементарный анализ на основе законов сохранения энергии и импульса показывает, что относительная доля энергии, которую  легкое тело массы m может передать тяжелому с массой M при упругом столкновении, не превышает 4m/M. В нашем случае эта доля составит не более 2∙10^-3 (масса электрона по крайней мере в 2000 раз меньше массы любого из атомов или молекул). Таким образом, очень много столкновений должно произойти, прежде чем электрон отдаст избыток своей энергии[9]. Чтобы убедиться, что это именно так, проведем подсчет.

 Запишем законы сохранения импульса и энергии для двух сталкивающихся лоб в лоб частиц с массами mи M соответственно. Пусть  m/M= ε <<1,   и до столкновения скорость легкой частицы υ=υ₀ , а тяжелой V₀=0.  Тогда

mυ₀= mυ₁+MV₁,                                                                          (10.17)

mυ₀²= mυ₁²+MV₁².                                                                      (10.18)

Здесь υ₁, V₁ скорости легкой и тяжелой частиц после столкновения. Возведем (10.17) в квадрат и разделим на m:

mυ₀²= mυ₁²+(M/ε)V₁²+2Mυ₁V₁.

А теперь вычтем из (10.18):

0=M(1-1/ε)V₁²-2Mυ₁V­_1,

и разделим на MV₁:

 V₁(1-1/ε)=2υ₁.                                                                              (10.19)

Из уравнения (10.17) имеем υ₁=υ₀-V₁/ε.  Подставляя в (10.19), получаем:

V₁(1-1/ε)=2υ₀-2V₁/ε,V₁(1+1/ε)=2υ₀,V₁=2ευ₀/(1+ε)≈2ευ₀.

Возведем последнее соотношение в квадрат и умножим на M/2:

MV₁²/2≈4εmυ₀²/2.

Таким образом, получаемая тяжелой частицей в результате упругого лобового столкновения кинетическая  энергия составляет всего лишь    от кинетической энергии легкой частицы. В остальных случаях передаваемая энергия еще меньше.

Рассмотрим теперь взаимодействие переменного электромагнитного  поля с одиночным свободным зарядом. Пусть напряженность электрического поля меняется во времени по закону E=E₀cosωt, где ω=2νπ - так называемая круговая частота, ν – частота электрического поля. Сила, действующая со стороны электрического поля на частицу  с массой  mи зарядом  e, равна .

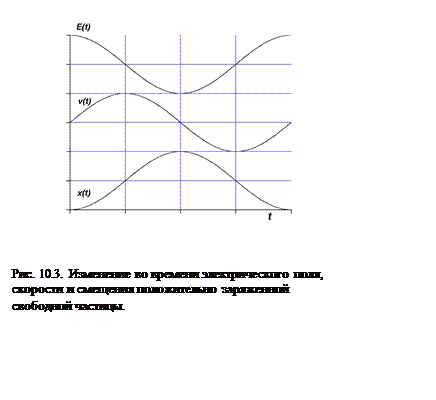
Из рисунка 10.3 видно, что скорость Vотстает от напряженности электрического поля на 90 градусов по фазе, а смещение заряженной частицы xпод действием электрического поля – на 180 градусов. Действительно, покоившаяся в начальный момент времени частица начинает увеличивать скорость в направлении поля. Рост скорости продолжается, пока сила не поменяет направление. Затем начинается торможение и уменьшение скорости до нуля. Таким образом, скорость частицы отстает от напряженности поля на четверть периода. По мере увеличения скорости частица начинает смещаться в положительном направлении, и это смещение продолжается, пока скорость частицы не упадет до нуля. Затем начнется движение в сторону исходного положения частицы. И здесь имеем отставание от скорости на четверть периода, а отставание от напряженности поля составляет половину периода.

Решение уравнения Ньютона для данной задачи приводит к 

                                     x=eE₀/mω²(1-cosωt),

то есть,   смещение x действительно находится в противофазе с напряженностью поля.