Принципы теплообменного оборудования. Пластинчато-ребристые теплообменники, страница 4

Чаще всего используют эмпирические или аналитические формулы, в которых коэффициент а выражен через числа Нуссельта или Стэнтона:

 ,

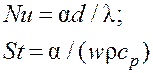связанные соотношением

Формулы для расчета теплообмена обычно имеют следующую структуру:

Nu=/(Re, Pr,K1, K2, ..., Кп); (24)

J = StPr2/3 =f(Re, K1 K2, …, Кп ).(25)       

Кроме чисел Рейнольдса Re =  и Прандтля Pr =, в эти формулы входят дополнительные критерии Кг, отражающие влияние геометрических и других факторов на теплообмен.

Эффективность (КПД) ребра .  Оребренные поверхности различного типа широко применяют в криогенных теплообменниках, обеспечивая создание высококомпактных развитых поверхностей. Наличие ребер несколько ухудшает процесс теплообмена (см. эпюру распределения температур на рис.5). Разность температур потока Т1 (или Т2) и ребра Тр максимальна у основания ребра, где Тр = Тс и минимальна у конца. Такое распределение температур обусловлено термическим сопротивлением ребра. В результате средняя  разность температур потока и ребра (Т — Тp)cp  меньше разности температур потока и стенки Т — Тс, что и определяет ухудшение теплообмена. Данное обстоятельство учитывают в расчетах введением  КПД ребра , который в соответствии с рис. 5 определяют так:

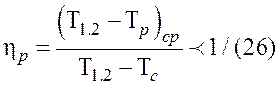
Расчетные формулы для определения  получают в результате решения уравнений теплопроводности для ребер различной конфигурации. Так, для прямых ребер

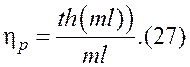
Здесь m — параметр ребра:

где  - коэффициент теплоотдачи; П и - периметр и площадь поперечного сечения ребра; -теплопроводность материала ребер.

Согласно рис. 6

.

На рис. 6 приведены зависимости, позволяющие определить значение  для прямых (r0/rвн = 1) и круглых (r0/rвн = 1,25 ... 3,00) ребер при разных радиусах r0 ребер. При ml  1 КПД ребер достаточно велик, что позволяет рекомендовать для выбора длины ребра соотношение.

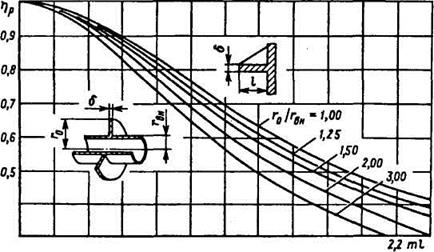Рис. 4.11. Зависимость эффективности (КПД) прямых и круглых ребер параметра ml (для круглого ребра l= r0 - rвн)

Формула (27) получена при условии Т = const, т. е. температура набегающего потока по длине ребра постоянна. Если принять другое граничное условие, а именно: Т — Тр = const — разность температур по ребру постоянна, то КПД можно определить по формуле

При ml < 1 расчет по формулам (27) и (29) дает близкие результаты. Для ребер сложной геометрической конфигурации, например в матричных теплообменниках, используют другие формулы Учитывая, что для гладкой стенки между ребер  =1, запишем выражение для КПД оребренной поверхности:

где Fp — площадь поверхности ребер.

Эти значения КПД вводят в формулы (21)—(22).

Гидродинамические потери в теплообменниках. Ограничения, налагаемые на потери давления , обусловливают ограничения на коэффициент теплоотдачи , поэтому тепловой и гидравлический расчеты тесно взаимосвязаны. Полные потери давления складываются из двух основных составляющих:, где         - потери давления на трение при течении вдоль поверхности теплообмена; - потери давления на местных сопротивлениях (сужение, расширение, повороты и т.п.).

Гидропотери , обусловленные трением, вычисляют по формуле

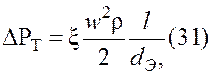
где  - коэффициент сопротивления, зависящий от характера потока, условий течения и геометрии канала:

w и р— средние значения скорости и плотности потока в канале; l и d3 — длина и эквивалентный диаметр канала.

Формулу (31) иногда записывают в другом виде. Подставив в формулу (31) значение эквивалентного диаметра канала d3 = 4FC/П = 4IFC/F, где Fc и П — площадь и периметр проходного сечения канала; F = Пl — площадь полной поверхности теплообмена, получаем

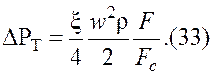
Здесь - фактор трения Фаннинга. При определении потерь давления на местных сопротивлениях обычно используют зависимость

Коэффициент местного сопротивления , определяют в зависимости от характера этого сопротивления и геометрических характеристик. Обычно

Коэффициенты сопротивлений  или , иногда выражают через число Эйлера: