Принципы теплообменного оборудования. Пластинчато-ребристые теплообменники, страница 12

Математическую модель рабочего процесса строят на основе дифференциального уравнения передачи теплоты по ребру

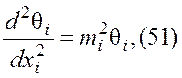
где q — разность температур потока () и ребра () в  i - м канале; х. — координата, отсчитываемая по высоте ребра от его корня в i-м канале; mi — параметр ребра

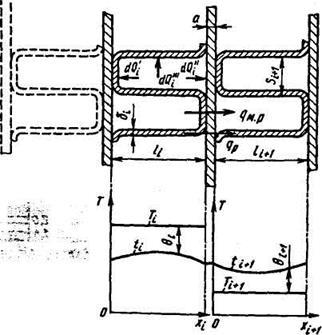
Рис. 19. Схема к расчету многопоточного теплообменника

Решение этого уравнения имеет вид

              (52)

где Сi’ и Сi" — постоянные интегрирования, определяемые из граничных условий.

Первое граничное условие: равенство температур ребер у их корней в двух смежных каналах (см. рис. 19). Например, в каналах i и i + 1 температуры ребер равны при xi = li и xi+1 = 0. Тогда из уравнений (52) найдем

                         (53)

Второе граничное условие: общее количество теплоты, переданное от потока к потоку на расчетном участке, представляет собой сумму количеств теплоты, переданной по ребрам () и через поверхность в межреберном пространстве (). Пренебрегая продольной теплопроводностью по стенке канала, тепловой баланс на расчетном участке можно записать в общем виде:

                                                       (54)

или по уравнению (55)

Из уравнений (52) и (55) найдем

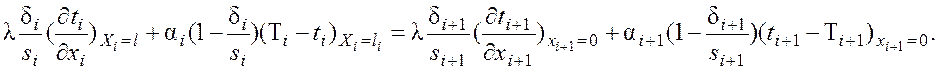
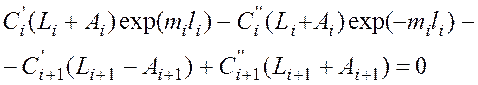                                 (56)

где

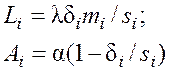                                               (57)

При числе каналов n систему уравнений для определения постоянных интегрирования С1¢, С1², С2¢, С2², … Сn¢, Сn² составляют на основе уравнений (53) и (56). Она включает 2n линейных уравнений с числом неизвестных постоянных интегрирования, также равным 2n. Определив постоянные интегрирования, находят поле температур в поперечном сечении по уравнению (52). Величину q иногда условно называют "избыточной" температурой ребра.

Уравнение теплового баланса для i-го канала без учета теплопритоков  (рис.19) имеет вид

                                        (58)

где  – тепловые потоки к одной и другой неоребренной сторонам канала;  – тепловой поток к ребрам канала; αi – коэффициент теплоотдачи, определяемый зависимостями (41);  qi¢ и qi² – температурные напоры между потоком и неоребренными сторонами канала; qi – средне-интегральный температурный напор между потоком и ребром; dFi – площадь поверхности теплообмена между ребрами на длине dh; dFpi – площадь поверхности теплообмена ребер на длине dh. Уравнение изменения энтальпии потока в i-м канале на длине dh:

.                         (59)

Решив уравнение (4.98) относительно производной, с учетом равенств     получаем систему обыкновенных нелинейных дифференциальных уравнений, описывающих изменение температуры потоков ПРТ по длине каналов:

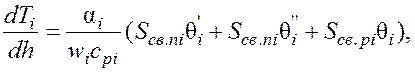                    (60)

где i = 1, …, n – число каналов ПРТ; G – массовый расход потока через канал; сpi – удельная теплоемкость потока на участке dh; w – массовая скорость потока.

Среднеинтегральная разность температур определяется следующим образом

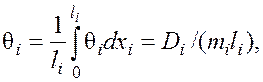                                 (61)

где

                           (62)

Для определения потерь давления систему (60) дополняют уравнением

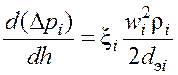                                       (63)

где xi = 4fi — коэффициент гидравлического сопротивления, пределяемый в соответствии с формулой (42).

Таким образом, задача расчета многопоточных ПРТ сводится к численному интегрированию системы (60) и (63) совместно с решением системы уравнений теплопроводности (53) и (56) на каждом шаге интегрирования. Граничные условия задаются в виде значений температур потоков на теплом и холодном концах теплообменника; значение потерь давления Dpi при dh = 0 принимают равным нулю. При достижении заданной температуры потоков интегрирование заканчивают и определяют длину пакета ПРТ L (см. рис. 11) и значения гидравлических сопротивлений по каждому потоку.