Принципы теплообменного оборудования. Пластинчато-ребристые теплообменники, страница 3

Рис. 4.9. Схема трехпоточного теплообменника при независимом теплообмене для каждой пары потоков

Сложный теплообмен с учетом взаимного влияния потоков рассмотрим на примере работы трехпоточного теплообменника типа «труба в трубе». Прямой поток движется в кольцевом зазоре (индекс 1), один из обратных потоков течет по внутренней трубе диаметром d2 (индекс 2), а другой омывает трубу диаметром d3 снаружи (индекс 3). Для 1-го участка уравнения теплового баланса имеют вид:

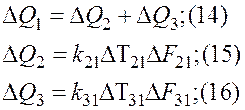
Из (15) и (16) имеем:

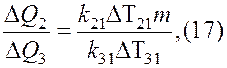
где

Исключив из уравнения (14) последовательно Q2 и Q3, с помощью соотношения (17) получаем расчетные зависимости, связывающие изменение энтальпий теплообменивающихся потоков (при этом Q определяем как G):

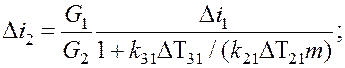
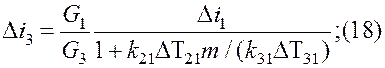
Расчет предусматривает использование диаграммы Q-Т, на которую наносят изобару прямого потока р1. Расчет ведут с концевого сечения аппарата, причем для каждого участка по заданному значению и вычисленным значениям к21 и к31 согласно (18) находят изменения энтальпий и , а также соответствующие им температуры по термодинамическим диаграммам. Это дает возможность построить изобары обратных потоков р2 и рг по аналогии с рис.1. Температуры и их разности на входе в каждый участок принимают постоянными для всего i-го участка. Построив диаграмму Q- T для всех трех потоков, нетрудно найти площади  элементов поверхности по участкам и для всего теплообменника в целом в соответствии с формулой (9). В частных случаях используют условие к21 / к31 = const, иногда учитывают теплоприток из окружающей среды.

Значительно сложнее метод расчета трехпоточных пластинчато-ребристых аппаратов. Основная поверхность этих аппаратов оребренная, а площадь поверхности ребра, участвующей в теплообмене со смежной секцией, меняется по длине аппарата, т.е. отношениеизменяется от сечения к сечению в зависимости условий теплообмена.

Коэффициент теплопередачи. При любых условиях теплообмена  необходимо знать коэффициент теплопередачи к, Вт/(м²∙К), являющийся сложной функцией условий теплообмена, свойств веществ, геометрических характеристик аппарата. В общем случае для аппарата с двусторонним оребрением схема теплообмена между двумя потоками с температурами Т1 и Т2, расходами G1 и G2, коэффициентами теплоотдачи  и приведена на рис.5, где F1 и F2 - площади поверхностей теплообмена со стороны каждого из потоков.

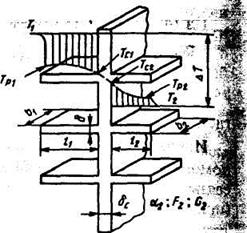Рис. 4.10. Схема теплообмена между двумя потоками для аппарата с двусторонним оребрением

Для аппарата в целом или отдельного i-го участка можно записать систему из трех уравнений передачи теплоты Q. от потока G1 к поверхности площадью F1 через стенку с Fc толщиной бс; от поверхности площадью F2 к потоку G2:

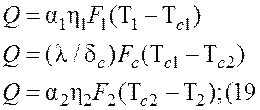
Здесь – КПД ребер, учитывающие градиент температур по длине каждого из ребер.

Решив эти уравнения относительно разностей температур

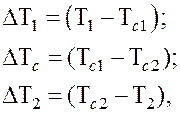
С учетом равенства из уравнения (19) получаем:

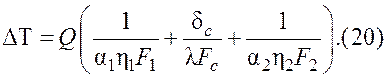
Приведя эту зависимость к виду (5), получим уравнения для коэффициентов теплопередачи к1 и к2, отнесенные соответственно к площадям поверхностей теплообмена F1 и F2:

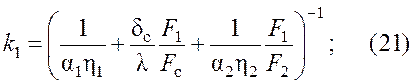
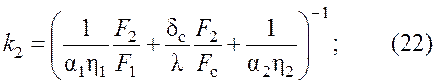
Строго говоря, формулы (21) и (22) записаны для плоских поверхностей, однако при малом отношении bjd их можно использовать для расчета трубок. Для разных типов аппаратов эти зависимости имеют разный вид. Так, для аппарата из тонких гладких трубок  без учета термического сопротивления стенки получаем

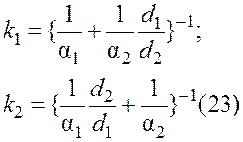
При определении коэффициентов к основные проблемы связаны с нахождением коэффициентов теплоотдачи и  Их вычисляют по различным формулам конвективного теплообмена в зависимости от условий протекания процесса (свободная конвекция, вынужденное движение, двухфазный процесс), характера потока (ламинарный, турбулентный, переходный, один из вариантов двухфазных потоков), геометрических характеристик аппаратов, влияния физических свойств теплоносителей и других факторов.