Выравнивание рядов распределения. Разработка двухфакторной модели. Оценка персонала с помощью нечетких множеств. Финансовый риск и неплатежеспособность

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ ТРАНСПОРТА»

Кафедра «Экономика транспорта»

Дисциплина

«Экономико – математические методы и модели»

Контрольная работа № 2

Выполнила                                                         

студентка 3 курса                                                           

заочного факультета                                           

учебный шифр 10-ЗБ-429                                

Легкая И.Н.                                                                                

Гомель 2013 г.

Задание № 1             «Выравнивание рядов распределения»

Требуется подтвердить гипотезу нормальности распределения эмпирического ряда величин себестоимости пропуска транзитных вагонов по участкам железных дорог и найти теоретическое нормальное распределение этих величин, для чего необходимо оценить величину расхождения между теоретическими и эмпирическими частотами.

Данные об интервальном изменении величин себестоимости пропуска вагонов  по участкам железных дорог, а также рассчитанные параметры  приведены в таблице 1.

Таблица 1 - Исходные данные и схема решения задачи

Границы интервала х		ni		*ni	-	(-)2	(-)2*ni	t	φ(t)	fi	fi-ni	(fi-ni)²	(fi-ni)²/fi
112	152	6	132	792	-192	36864	221184	-1,72	0,0909	6,87	0,87	0,76	0,11
152	192	6	172	1032	-152	23104	138624	-1,37	0,1561	11,79	5,79	33,52	2,84
192	232	11	212	2332	-112	12544	137984	-1,01	0,2396	18,09	7,09	50,2	2,77
232	272	20	252	5040	-72	5184	103680	-0,65	0,3271	24,71	4,71	22,18	0,89
272	312	40	292	11680	-32	1024	40960	-0,29	0,3825	28,89	-11,11	123,43	4,27
312	352	56	332	18592	8	64	3584	0,07	0,3980	30,06	-25,94	672,88	22,38
352	392	20	372	7440	48	2304	46080	0,43	0,3637	27,47	7,47	55,80	2,03
392	432	20	412	8240	88	7744	154880	0,79	0,2920	22,06	2,06	4,24	0,19
432	472	14	452	6328	128	86384	1209376	1,15	0,2059	15,55	1,55	2,40	0,15
472	512	13	492	6396	168	28224	366912	1,51	0,1276	9,64	-3,36	11,29	1,17
512	552	4	532	2128	208	43264	173056	1,87	0,0694	5,24	1,24	1,54	0,29
-	-	210	-	70000	-	-	2596320	-	-	200,37	-	-	37,09

Решение:

1. По данным граф 1 и 2 строим гистограмму распределения величин рентабельности отделений железных дорог по их частоте. Если считать, что частоты распределены внутри каждого интервала равномерно, то получается, что частота любого интервала приближенно равна площади прямоугольника. (Рисунок 1.1)

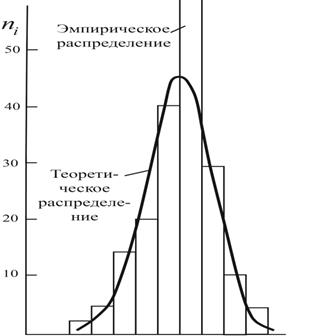
             112   152   192   232   272  312   352  392  432    472 

Рисунок 1.1 – Гистограмма эмпирического ряда

2. Таблица 1.1.

а) средние значения рентабельности в интервале:

=        

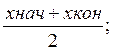
где х_нач. – начальная величина в интервале;

      х_кон. – конечная величина в интервале;

б) средние значения всего ряда рентабельности:

 =  ;              =

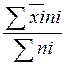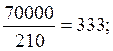
            в) среднеквадратичное отклонение:

;     

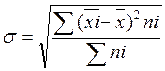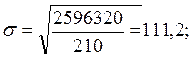
3. Нормальное отклонение рассчитывается по формуле:

     t =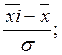

4. Частоты теоретического нормального распределения определяются следующим образом:

Величина: 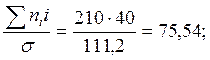                   fi=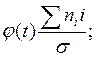

5. Сумма теоретических частот сравнивается с суммой частот эмпирического распределения . Расхождение между Ʃfі = 200,37  и  Ʃnі = 210  значительное 9,63%, гипотеза отвергается.

6. Расчет величины «хи – квадрат»:

      Х²р =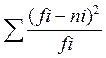= 37,09;

7. Найдем число степеней свободы r:

    r = R – 3;

R – число интервалов в фактическом распределении;

   r = 11 – 3 = 8;

Х²t – согласно соответствующем уровне значимости = 15,5;

          Если Х²р  Х²t, то гипотеза о форме выравнивающей кривой распределения, не отвергается и расхождения  между теоретическими и эмпирическими частотами относятся за счет влияния случайных обстоятельств.

          Если   Х²р > Х²t, то гипотеза о форме теоретического распределения считается неправильной.

          В нашем случае 37,09 > 15,5, следовательно, гипотеза о форме теоретического распределения считается неправильной.

Рассчитаем критерий согласия:

Rr= 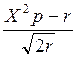= 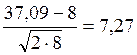> 3 .

          Таким образом, гипотеза неправильности выравнивания эмпирического ряда теоретической нормальной кривой подтверждается этим критерием.

Задание № 2                     «Разработка двухфакторной модели»

            Установить параметрыдвухфакторной модели определения эксплуатационных расходов то передвижению  груженых вагонов по двухпутным электрифицированным  участкам сети в зависимости от влияния двух факторов — профиля пути на этих участках и расходной ставки на 1 кВт.ч; оценить адек­ватность полученной модели и рассчитать величину коэффи­циента множественной регрессии.

          Данные для моделирования влияния двух факторов на величину эксплуатационных расходов по пропуску груженных вагонов приведены в таблице 2.

Таблица 2 – Исходные данные и схема определения многофакторной модели

у	х1	х2	х21	х1х2	х22	ух1	ух2	у-	yx	(y-)2	y-	(y-)2	y-yx	(y-yx)/y
1,16	0,7	0,74	0,49	0,518	0,547	0,812	0,858	0,01	1,025	0,0001	0,011228	0,000126073	0,13492	0,11631
1,08	1,2	0,74	1,44	0,888	0,547	1,296	0,799	-0,06	1,041	0,0036	-0,06877	0,004729556	0,03892	0,036037
1,12	1	0,78	1	0,78	0,608	1,12	0,873	-0,02	1,057	0,0004	-0,02877	0,000827814	0,06204	0,055393
0,98	0,6	0,79	0,36	0,474	0,624	0,588	0,774	-0,17	1,051	0,0289	-0,16877	0,028483909	-0,07098	0,072429
1,06	1	1,03	1	1,03	1,061	1,06	1,092	-0,09	1,203	0,0081	-0,08877	0,007880426	-0,14346	0,13534
1,75	0,6	1,08	0,36	0,648	1,166	1,05	1,89	0,60	1,219	0,3600	0,601228	0,361475391	0,53024	0,302994
1,06	0,1	1	0,01	0,1	1,06	0,106	1,06	-0,09	1,157	0,0081	-0,08877	0,007880426	-0,0972	0,091698
1,15	0,7	1,07	0,49	0,749	1,145	0,805	1,231	0	1,217	0	0	0	-0,06714	0,058383
1,27	1,1	1,14	1,21	1,254	1,299	1,397	1,448	0,12	1,271	0,0144	0,121228	0,014696285	-0,00068	0,000535
1,1	0,4	1,01	0,16	0,404	1,020	0,44	1,111	-0,05	1,173	0,0025	-0,04877	0,002378685	-0,07262	0,066018
1,1	1,9	1	3,61	1,9	1,1	2,09	1,1	-0,05	1,215	0,0025	-0,04877	0,002378685	-0,1148	0,104364
1,1	-0,7	1,03	0,49	-0,721	1,061	-0,77	1,133	-0,05	1,149	0,0025	-0,04877	0,002378685	-0,04906	0,0446
1,44	1,6	1,16	2,56	1,856	1,346	2,304	1,670	0,29	1,298	0,0841	0,291228	0,084813885	0,14168	0,098389
1	-0,4	0,74	0,16	-0,296	0,547	-0,4	0,74	-0,15	0,989	0,0225	-0,14877	0,022133038	0,01012	0,01012
1	0,7	0,77	0,49	0,539	0,593	0,7	0,77	-0,15	1,043	0,0225	-0,14877	0,022133038	-0,04254	0,04254
1,06	0,8	1	0,64	0,8	1,06	0,848	1,06	-0,09	1,179	0,0081	-0,08877	0,007880426	-0,1196	0,11283
1,09	1,2	1,08	1,44	1,296	1,166	1,308	1,177	-0,06	1,239	0,0036	-0,05877	0,00345412	-0,14896	0,136661
19,52	12,5	16,16	15,91	12,219	15,95	14,754	18,7871	0,03	19,53	0,5737	-	0,573651951	-0,00912	1,48464

Решение:

Линейная модель имеет вид: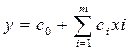       

где  с – параметр, не зависящий от исследуемых факторов;

       с1 – параметры, определяющие количественное влияние каждого фактора на величину функции;

       xi – факторы – аргументы.

       Для  случая, когда на функцию у, характеризующую изучаемое явление, влияет изменение одновременно двух факторов х1 и х2, система уравнений имеет вид:

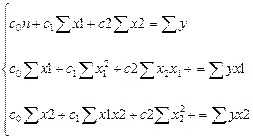
17с0 + 12,5с1 + 16,16с2 = 19,52;

12,5с0 + 15,91с1 + 12,2с2 = 14,75;

16,16с0 + 12,2с1 + 15,73с2 = 18,78.

с0 = 0,572;

с1 = 0,032;

с2 = 0,582.

Определив с0 , с1, с2 найдем искомую модель:

у = 0,572 + 0,032х1 + 0,582х2.

Для оценки адекватности модели можно использовать и показатели средней ошибки аппроксимации    (в %).

Рассчитываем средние фактического и теоретического ряда величин эксплуатационных расходов:

    

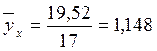
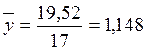
Оцениваем точность модели – степень приближения теоретической поверхности регрессии к фактическим значениям:

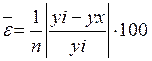
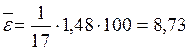 = 9%.

На оценку адекватности влияют выбор формы модели, число наблюдений