Экономико-математические методы и модели: Учебно-методическое пособие по выполнению контрольной работы № 2

переменных, можно изобразить в виде различных моделей (подробнее [3, с. 16] или [4, с. 137]). На практике наибольшее распространение получили линейные и приведенные к линейным модели. Основным достоинством линейных моделей является их простота, а методика их решения доступнее и лучше разработана.

Линейная модель имеет вид

,

где  – параметр, не зависящий от исследуемых факторов;

 – параметры , определяющие количественное влияние каждого фактора на величину функции, ;

 –  факторы-аргументы.

Параметры модели находятся в ходе решения системы нормальных уравнений, например, методом наименьших квадратов. Для случая, когда на функцию у, характеризующую изучаемое явление, влияет изменение одновременно двух факторов и , система уравнений имеет вид:

                                  

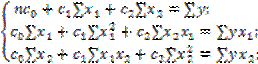
Определив  и  найдем искомую модель

.

Для оценки адекватности модели можно использовать и показатели средней ошибки аппроксимации, %.

Одновременное влияние независимых переменных  на зависимую переменную у измеряется коэффициентом множественной регрессии R. Чем меньше наблюдаемые величине отклоняются от поверхности множественной регрессии, тем больше значение  R. Для линейной модели

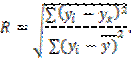
При небольшом числе наблюдений величина выборочного коэффициента множественной корреляции обычно завышается. Поэтому величину R корректируют.

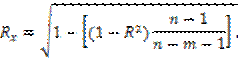
Пример. Рассмотрим процесс моделирования на примере определения эксплуатационных расходов по передвижению грузовых вагонов по двухпутным электрифицированным участкам сети у, если известны величины эквивалентных уклонов , характеризующих профиль пути соответствующих участков, и расходная ставка на 1кВт ∙ ч электроэнергии . Для нахождения многофакторной модели используются исходные данные, приведенные в таблице 2.2. Там же дан порядок расчета промежуточных величин. Используя итоговые данные граф 2 – 9 таблицы 2.2, запишем искомую систему уравнений в виде:

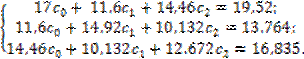
Решив эти уравнения, получим ,  и . Следовательно искомая двухфакторная модель записывается так:

.

Определяем все теоретические значения , которые для нашего примера приведены в графе 11. Затем рассчитываем средние фактического и теоретического ряда величин эксплуатационных расходов:

Оцениваем точность модели – степень приближения теоретической поверхности регрессии к фактическим значениям:

На оценку адекватности влияют выбор формы модели, число наблюдений и точность расчетов. Расчетная средняя ошибка получилась равной 13%, что свидетельствует о недостаточно высокой точности модели.

Таблица 2.2 – Иcходные данные и схема определения многофакторной

модели

Номер наблюдения	y
	1	2	3	4	5	6	7	8
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17	1,16 1,08 1,12 0,98 1,06 1,75 1,06 1,15 1,27 1,10 1,10 1,10 1,44 1,00 1,00 1,06 1,09	0,7 1,2 1,0 0,6 0,1 0,6 0,1 0,7 1,1 0,4 1,9 –0,7 1,6 –0,4 0,7 0,8 1,2	0,64 0,64 0,68 0,69 0,93 0,98 0,90 0,97 1,04 0.91 0,90 0,93 1,06 0,64 0,67 0,90 0,98	0,49 1,44 1,00 0,36 0,01 0,36 0,01 0,49 1,21 0,16 3,61 0,49 2,56 0,16 0,49 0,64 1,44	0,448 0,768 0,680 0,414 0,093 0,588 0,090 0,679 1,144 0,364 1,710 –0,651 1,696 –0,256 0,469 0,720 1,176	1,410 0,410 0,462 0,476 0,865 0,960 0,810 0,941 1,082 0,828 0,810 0,865 1,124 0,410 0,449 0,810 0,960	0,812 1,296 1,120 0,588 0,106 1,050 0,106 0,805 1,397 0,440 2,090 –0,770 2,304 –0,400 0,700 0,848 1,272	0,742 0,691 0,762 0,676 0,986 1,715 0,954 1,116 1,321 1,001 0,990 1,023 1,526 0,640 0,670 0,954 1,068
	19,52	11,6	14,46	14,92	10,132	12,672	13,764	16,835

Продолжение таблицы 2.2

Номер наблюдения
	9	10	11	12	13	14	15
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17	0,01 0,07 –0,03 0,17 –0,09 0,60 –0,09 0,00 0,12 –0,05 –0,05 –0,05 0,29 –0,15 –0,15 –0,09 –0,06	0,92 0,95 0,98 0,97 1,23 1,31 1,20 1,30 1,39 1,22 1,25 1,21 1,43 0,89 0,95 1,22 1,32	0,0001 0,0049 0,0009 0,0289 0,0081 0,3600 0,0081 0,0000 0,0144 0,0025 0,0025 0,0025 0,0841 0,0225 0,0225 0,0081 0,0036	0,00 –0,08 –0,04 –0,18 –0,10 0,59 –0,10 –0,01 0,09 –0,06 –0,06 –0,06 0,28 –0,16 – 0,16 –0,10 –0,07	0,0000 0,0064 0,0016 0,0324 0,0100 0,3481 0,0100 0,0001 0,0081 0,0036 0,0036 0,0036 0,0784 0,0256 0,0256 0,0100 0,0049	0,24 0,13 0,14 0,01 –0,17 0,44 –0,14 –0,15 –0,12 –0,12 –0,15 –0,11 0,01 0,11 0,05 –0,16 –0,23	0,20 0,12 0,12 0,01 0,16 0,25 0,13 0,12 0,09 0,11 0,14 0,10 0,01 0,11 0,05 0,15 0,21
	0,45	19,74	0,5737	–	0,5720	–0,22	2,22

Находим теперь величину коэффициента множественной регрессии.

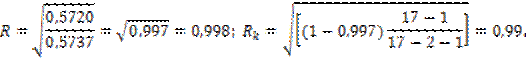
Величина  подтверждает, что модель может использоваться для экономических расчетов.

3 НЕЧЕТКИЕ МНОЖЕСТВА В РЕШЕНИИ

ЭКОНОМИЧЕСКИХ ЗАДАЧ

ПРИ УПРАВЛЕНИИ ПРЕДПРИЯТИЕМ

3.1 0ценка персонала с помощью нечетких множеств

3.1.1 Исходные данные

Исходные данные для решения задачи даны в приложении Б. Вариант исходных данных принимается по последней цифре шифра.

2.1.2 Методические указания

Оценка возможностей персонала для выполнения определенных задач или для его ориентации на другие задачи является важной проблемой для предприятия. Поскольку речь идет о многокритериальной проблеме с де­терминированными нечеткими данными, она подпадает под действие тео­рии нечетких множеств. Предположим, что существует 8 видов деятельности

                                           (3.1)

и эксперту по отбору задают вопрос об оценке качеств кандидата относи­тельно каждого из 8 видов деятельности, выражаемых десятичными дробя­ми от 0 до 1. Отметим, что некоторые виды оценки будут иметь субъективный характер, в то время как другие могут быть измеримыми.

Несмотря на это, они должны расположиться на одной и той же шкале. Таким образом, значение, которое дается квалификацией кандидата p, будет обозначаться нечетким подмножеством из интервала [0,1], напри­мер:

Представим, что на месте работы t требуются различные уровни квали­фикации для каждого из видов деятельности .Эти уровни квалификации также образуют нечеткое подмножество

Построим коэффициент адекватности р относительно t следующим об­разом. Если

                                                (3.4)

то запишем

Если

                                                (3.5)

то запишем

или в более общей форме

 Так, применяя (3.4) и (3.5) к (3.2) и (3.3), получаем коэффициент адекватности  как результат суммирования  и деления суммы на мощность , для получения числа в отрезке [0,1 ]:

          (3.6)

Эта система оценки не имеет в виду необыкновенные возможности