Задача определения оптимального режима движения поезда по участку

Задача определения оптимального режима движения поезда по участку

Постановка задачи:

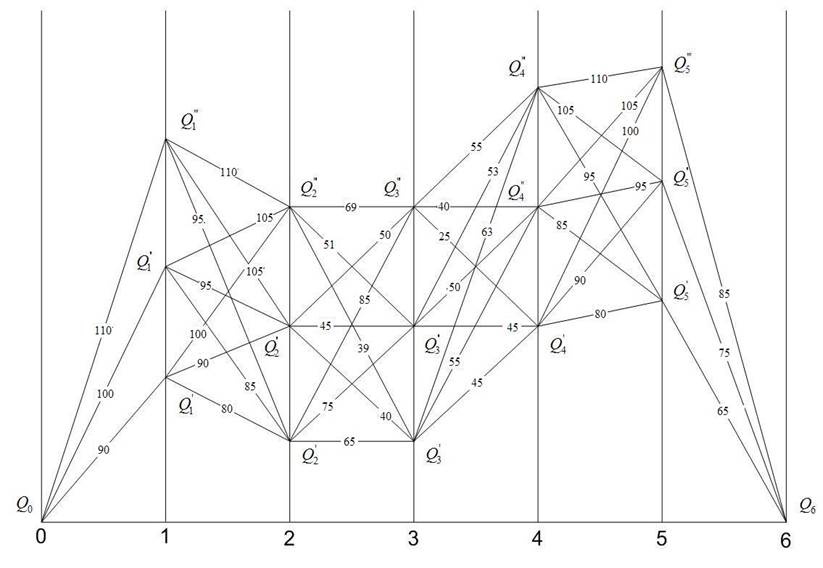
На рисунке показан профиль участка, состоящий из шести элементов. Движение поезда начинается с первого элемента. В зависимости от режима ведения по этому элементу кривая скорости может попасть в некоторое число точек на вертикали 1. Фиксируем на ней все возможные значения скорости через интервал в 1 км/ч. Для простоты рассмотрим только три такие точки. Аналогичным образом на остальных вертикалях будем фиксировать значения скорости.

Необходимо определить такой режим следования поезда на отрезках пути, который обеспечил бы минимальные приведенные расходы на передвижение по участку в целом. Эти расходы зависят от скорости поезда и от сопротивления его движению, которое в свою очередь зависит от профиля пути. Поэтому в качестве вычислительного этапа можно рассматривать элемент профиля пути с одинаковым уклоном.

Этап условной оптимизации:

Из точек на вертикали 1 можно попасть в каждую точку на вертикали 2, соблюдая определенный режим движения и реализуя определенные затраты. Эти затраты показаны на линиях, соединяющих соответствующие точки. Их подсчитывают заблаговременно на каждом элементе пути для всех вариантов движения на основе тяговых расчетов. Начинаем решать задачу с последней точки пути поэтапно. На вертикаль 5 поезд может вступить с тремя значениями скорости. Каждому из них однозначно соответствуют приведенные расходы на передвижение поезда по данному элементу до остановки. Выделяем три условно-оптимальных стратегии:               

F₅^’=65; F₅^’’=75; F₅^’’’=85

На вертикаль 4 поезд может вступить также с тремя значениями скорости. Но и двигаться оно может из каждой точки на вертикали 5 в одну из трех точек на вертикали 4 также по трем вариантам (тремя режимами). Находим условно оптимальные стратегии на этом элементе, сравнивая между собой все варианты движения судна по минимуму общих расходов на обоих элементах пути:

F₄^’=min(80+65; 90+75; 100+85)=145;

F₄^’’=min(85+65; 95+75; 105+85)=150;

F₄^’’’=min(95+65; 105+75; 110+85)=160;

Аналогично находим условно оптимальные стратегии на следующем элементе :

F₃^’=min(45+145; 55+150; 63+160)=190

F₃^’’=min(45+145; 50+150; 53+160)=190;

F₃^’’’=min(25+145; 40+150; 55+160)=170

Аналогично находим условно оптимальные стратегии на следующем элементе :

F₂^’=min(65+190; 75+190; 85+170)=255;

F₂^’’=min(40+190; 45+190; 50+170)=220;

F₂^’’’=min(39+190; 51+190; 69+170)=129;

На предпоследнем этапе расчетов

F₁^’=min(80+255; 90+120; 100+129)=210;

F₁^’’=min(85+255; 95+120; 105+129)=234;

F₁^’’’=min(95+255; 105+120; 110+129)=225;

Этап безусловной оптимизации

Поскольку начальное состояние системы задано однозначно, на этапе определяем оптимальные режимы движения поезда для каждого элемента пути и минимальные приведенные затраты на движение из начального пункта пути в конечный.

F=min(90+210; 100+215; 110+225)=300;

Вывод:

При следовании поезда по пути приведенному на графике расходы будут минемальными и составят 300 ден. ед.