Решение задачи о назначениях венгерским методом
Постановка задачи:
Пусть управление механизации имеет 5 кранов. Требуется возвести 5 объектов. Известна себестоимость строительства каждым краном отдельного объекта. Требуется так распределить краны по объектам, чтобы обеспечить возведение всех объектов с минимальными суммарными затратами.
|
Краны |
Комплекс работ |
||||
|
Строительство 1-го объекта, В1 |
Строительство 2-го объекта, В2 |
Строительство 3-го объекта, В3 |
Строительство 4-го объекта, В4 |
Строительство 5-го объекта, В5 |
|
|
Себестоимость строительства |
|||||
|
Кран 1, А1 |
66,0 |
20,0 |
42,0 |
49,0 |
26,0 |
|
Кран 2, А2 |
46,0 |
40,0 |
79,0 |
43,0 |
38,0 |
|
Кран 3, А3 |
74,0 |
49,0 |
31,0 |
40,0 |
22,0 |
|
Кран 4, А4 |
20,0 |
77,0 |
65,0 |
21,0 |
68,0 |
|
Кран 5, А5 |
51,0 |
58,0 |
19,0 |
11,0 |
17,0 |
Определим тип задачи о назначениях. Количество исполнителей равно пяти, количество работ тоже пяти, следовательно, данная задача является задачей закрытого типа.
Построим математическую модель задачи.
Обозначим через ![]() - назначение
- назначение ![]() -го исполнителя на
-го исполнителя на ![]() -й вид работ,
-й вид работ, ![]() -
стоимость выполнения
-
стоимость выполнения ![]() -й работы
-й работы ![]() -м исполнителем соответственно.
-м исполнителем соответственно.
Математическая модель задачи примет вид:
найти план назначений 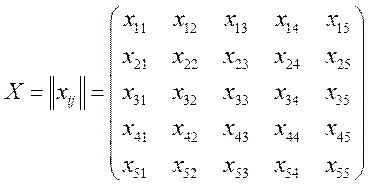
при следующих ограничениях:
1. Каждый исполнитель назначается только на одну работу:
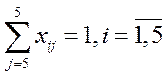
2. Каждый исполнитель назначается только на одну работу:
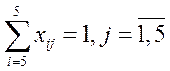
условие целочисленности:
![]()
где переменные ![]() ,
если
,
если ![]() вид работ выполняется
вид работ выполняется ![]() исполнителем,
исполнителем, ![]() -
в остальных случаях,
-
в остальных случаях,
и чтобы общая стоимость возведения 5-ти объектов была минимальна:
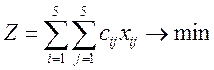
Составим матрицу стоимостей выполнения работ:
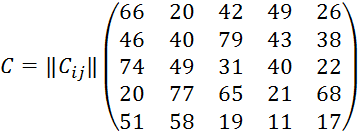
Находим минимальный элемент в каждой строке исходной матрицы:
![]() min
min
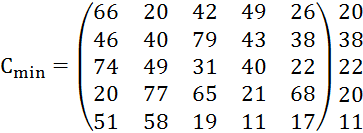
Затем вычитаем минимальные элементы из
всех элементов соответствующих строк и находим минимальные элементы в столбцах
новой матрицы:
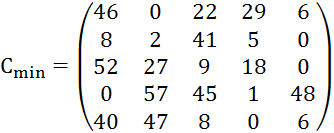
![]()
![]()
Вычитаем данные элементы из соответствующих столбцов матрицы:
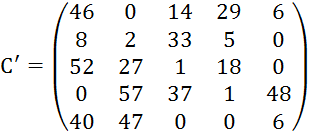
Проверка решения на оптимальность.
Выбираем строку, содержащую минимальное количество нулей, один из них помечаем *. Вычеркиваем все нули этой строки и этого столбца. Аналогичные операции выполняем для всех строк.
![]()
![]()
![]()
![]()
![]()
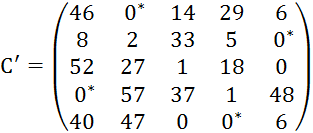
План не оптимален, так как не построена система из n=5 независимых нулей.
Далее находим минимальный невычеркнутый элемент, в данном случае 1. Его отнимаем от всех невычеркнутых элементов и прибавляем его к элементам стоящим на пересечении проведенных прямых и производим проверку оптимальности.
![]()
![]()
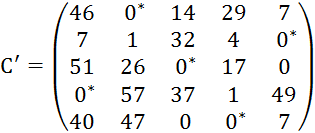
План является оптимальным, так как построена система из n=5 независимых нулей.
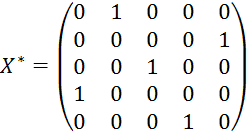
z(x*)=20+31+38+20+11=120 ден. ед.
Вывод: необходимо назначить первый кран на строительство 2-го объекта, второй на строительство 5-го, третий кран на 3-й объект, четвертый на строительство 1-го, а пятый кран на строительство 4-го объекта. При этом себестоимость минимальна и составляет 120 ден. ед.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.