Фильтрация изображений. Изучение предварительной обработки видеоданных (Лабораторная работа № 5)

Лабораторная работа №5

Фильтрация изображений

Цель работы: Изучение предварительной обработки видеоданных.

Необходимые теоретические сведения

5.1 Понятие фильтрации

Понятие фильтрации в данном случае весьма обширно, и включает в себя любое преобразование графической информации. Фильтрация может быть задана  не только в виде формулы, но и в виде алгоритма, его реализующая. Человек запоминает графическую информацию, в основном, в виде трех ее составляющих

1.  Низкочастотные составляющие изображения. Они несут информацию о локализации объектов, составляющих изображения. Эта составляющая наиболее важна, так как связка глаз - мозг уделяет ей первостепенное внимание.

2.  Высокочастотные составляющие изображения. Они отвечают за цветовые перепады - контуры изображения. Увеличивая их, мы повышаем резкость изображения.

3.  Текстуры изображения. Можно трактовать текстуру как характеристику участков в контурах изображения.

5.2 Операции над изображениями

Изображение в компьютере представляется в виде матрицы элементов изображения размером M×N, где М – количество строк, а N – количество элементов в строке (Рис.5.3). Элемент изображения (пиксел)/с координат (х,у) имеет свое значение интенсивности (яркости) u=f(x,y). Все возможные значения изображения f(x,y) могут принимать G значений уровня, G > 2 Нулевому уровню G соответствует черный цвет, а уровню G – 1 – белый. На практике чаще всего используется 256 уровней яркости G, т.к. для отображения любого допустимого значения уровня достаточно 8 бит. При G > 2 изображение называется полутоновым, а при G = 2 – бинарным.

Несколько бинарных или полутоновых изображений могут обрабатываться как многоканальное изображение. Такие изображения имеют место при обработке видеоданных в различных спектральных диапазонах и системах цветного изображения. При совместной обработке изображений f₁, f₂, ..., f_n значения функции изображения определяется как некоторый вектор

f(x,y) = (f₁(x,y), f₂(x,y),...,f_c(x,y)),

где f_i(x,y) – значение яркости в i – м канале, для i = 1, 2, ..., c; с – количество каналов. Рассмотрим основные характеристики цифровых изображений.

Среднее значение интенсивности изображения, вычисляемое по формуле

.

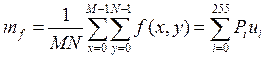где u_i – i – й уровень серого; P_i – вероятность появления i – го уровня. Среднее значение в определенной степени свидетельствует о том, является ли изображение более светлым или более темным. Однако по нему нельзя судить о контрастности, которая определяется разностью между максимальным и минимальным уровнями пикселов всего изображения.

Для характеристики контрастности изображения используют среднее значение квадрата отклонения величины текущего пиксела от среднего значения интенсивности

С целью упрощения вычисления среднего квадрата отклонения обычно пользуются формулой

.

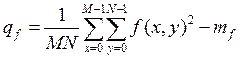В случае многоканальных изображений для характеристики средней, интенсивности и среднего квадрата отклонения применяют соответственно векторы

m_f = (m_f0, m_f1, …, m_fC–1)

и

q_f = (q_f0, q_f1, …, q_fC–1).

Для характеристики распределения уровней полутонового изображения применяется гистограмма относительных частот появления определенных Уровней в изображении. Относительная частота интенсивности g – го уровня пиксела определяется как

P_f(g) = n_g/(MN); при g = 0,1,..., G – 1,

где n_g – количество элементов изображения с уровнем g. Очевидно, что 0 ≤ P_f(g) ≤ 1.

Статистика распределения полутонов и, следовательно, гистограммы являются основой для так называемых точечных операций, которые могут изменять это распределение. В зависимости от вида гистограммы различают (Рис.5.4,а) – унимодальные (одногорбовые), (Рис.5.4,б) – бимодальные (двугорбовые) и мультимодальные распределения (Рис.5.4,в). Вид распределения играет существенную роль в задачах изменения контрастности и сегментации изображений.

Для оценки среднего информационного содержания изображения используется его энтропия

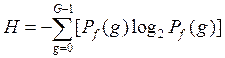
Если в состав некоторого фрагмента изображения входят элементы с одинаковым уровнем, то его называют гомогенным. Для гомогенного изображения справедливо соотношение

P_f(g) = 1 при g = g_k ;

P_f(g) = 0 в противном случае.

При выполнении многих операций над изображениями часто используются точки цифрового изображения, окружающие данный пиксел. Множество точек, соседних по отношению к заданной, называются окрестностью NSi. Здесь буквой i обозначается количество точек окрестности. Так например, 4 – точечная окрестность NS4 (Рис.5.5,а) определяется выражением

а 8 – точечная окрестность (Рис.5.5,б). NS8 – выражением

NS8(x, y) = {(х – 1, у + 1), (х – 1, у)(х – 1, у – 1), (х, у +1), (x, y – 1), (x + 1, y + 1), (x + 1, y), (x + 1, y–1)}.

Приведенные выше определения окрестностей не включают центральной точки (х,у). В ряде случаев целесообразно включать в рассмотрение и ее. Тогда имеем

NS5(x, y) = NS4(x, y) U {(x, y)}

и

NS9(x, y) = NS8(x, y) U {(x, y)}.

Аналогично можно определить и другие окрестности.