Фильтрация изображений. Изучение предварительной обработки видеоданных (Лабораторная работа № 5), страница 6

S_x = f(x+1, y) – f(x, y);      S_y = f(x, y+1) – f(x, y).

Соответствующие окна для определения первой производной в направлениях x и y изображены на рис. 5.10.

Существует много операторов, полученных из градиентных и служащих для обнаружения границ. Одним из простейших является оператор Робертса, который определяется следующим образом

f_p(x, y) = max[|f(x, y) – f(x+1, y)|, |f(x+1, y) – f(x, y + 1)|],

или приближенно

f_p(x, y) = |f(x. y) – f(x+1, y+1)| + |f(x+1,y) – f(x, y+1)| .

Так, например, полагая, что после обработки фрагмента изображения (рис.5.11,а), который окружен нулями, с помощью оператора Робертса получим выходной фрагмент (рис.5.11 ,б).

Кроме этого, широко применяются операторы Превита (Рис.5.12,а), Собела (Рис.5.12,б), ряд операторов Кирша (Рис.5.12,в ).

Рассмотренные выше дифференциальные операторы выделяют более сильно вертикальные или горизонтальные линии, т.е. они зависимы от направления.

Другим видом зависимых от направления операторов являются так называемые компасс–градиентные (Рис.5.13). Название географического направления говорит о направлении перепада, которое вызывает максимальный отклик фильтра.

Для обнаружения линий или для фокусировки изображений во многих случаях целесообразно использовать оператор Лапласа (лапласиан), который вычисляет вторую производную функции. Для непрерывных функций он представляется в виде

.

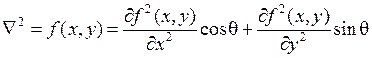На практике лапласиан вычисляется по приближенной формуле

Оконная функция Лапласиана имеет вид, представленный на рис.5.14,а. Часто вместо нее используют также функции рис.5.14,6 и рис.5.14,в.

Оператор Лапласа обладает инвариантностью к повороту изображений, т.е. на одном и том же изображении он дает один и тот же результат независимо от ориентации этого изображения.

Эффект улучшения резкости изображения достигается за счет того, что сначала изображение усредняется, а затем из него вычитается исходное. В результате линии границ на изображении становятся более резкими.

Следовательно, на исходном изображении границы усиливаются, т.к. к ним прибавляются высокочастотные компоненты. Поэтому вычитание лапласиана из исходного изображения приводит к улучшению фокусировки последнего. Обычно такой же эффект дает вычитание из исходного изображения взвешенного среднего.

Указания к выполнению

Вывод изображения bmp из файла на экран: Вставка > Рисунок. И в левом нижнем углу появившейся области указать в кавычках путь к файлу, например “d:\4.bmp”

Чтение изображения bmp в матрицу выполняется командой T:=READBMP(“путь_к_файлу\имя файла”).

Вывод изображения bmp из матрицы на экран T=.

Для произведения операций необходимо знать размер прочитанного изображения (размерность матрицы - маткад сам выделит необходимый объем памяти). Для этого используются команды:

Возврат числа строк матрицы <имя переменной>:=rows(<имя матрицы>)

Возврат числа столбцов матрицы <имя переменной>:=cols(<имя матрицы>)

Изображение выведенное из матрицы будет в градациях серого с максимальной яркостью 255. Для его преобразования в черно-белое можно использовать разные принципы, например, все значения яркости меньше половины максимального обнулить, а всем значениям выше половины-присвоить максимальное значение.

Порядок выполнения работы

Данная работа выполняется на ПЭВМ с использованием программы MathCAD 2000.

1.  Вывести его на экран с диска заданный преподавателем файл.

2.  Считать с диска заданный преподавателем файл в матрицу и вывести его на экран.

3.  Преобразовать изображение в черно-белое.

Оформление отчета

В отчете необходимо представить исходное изображение и выпорлненные преобразования над ним.