Нормирующий коэффициент оконных функций выбирается т.о., чтобы процедура подавления шума не вызывала смещение средней интенсивности обработанного изображения.
Существенным недостатком линейной фильтрации изображений является то, что наряду с уменьшением шумов одновременно происходит размывание контуров изображения. Это вызвано тем, что все элементы исходного изображения обрабатываются с одинаковым коэффициентом, т.е. линейные фильтры являются независимыми от структуры элементов и поэтому они не могут определить разницу между зашумленными и контурными элементами.
Чтобы уменьшить размывание изображения, целесообразно использовать метод селективного сглаживания. В ряде случаев, если яркость пикселов входного изображения распределена по нормальному закону, весьма эффективной при проведении предварительной обработки может оказаться сигма–фильтрация, при которой учитываются только те элементы входного изображения (находящиеся внутри окна), яркость которых находится в пределах Ех ±2 σ. Здесь Ex – математическое ожидание, а σ – среднеквадратическое отклонение яркости пикселов изображения.
5.3.3 Нелинейная локальная фильтрация
Основное отличие нелинейной фильтрации от линейной заключается в том, что выходной сигнал формируется нелинейным образом от данных исходного изображения, а для рекурсивной фильтрации – нелинейным образом от отфильтрованного на предыдущих шагах изображения. В системах обработки изображения наиболее широкое применение находят два класса нелинейных фильтров. Фильтры, относящиеся к первому классу, используются для подавления шумов, а фильтры второго класса – для подчеркивания перепадов яркости. Весьма эффективным методом для подавления шумов является медианная фильтрация, в процессе которой сначала производится сортировка по величине пикселов, попавших в окно фильтра, а затем замена значения опорной точки (х, у) величиной яркости пиксела, расположенного в середине (на медиане) этого ряда. В связи с этим медианный фильтр не оказывает влияние на ступенчатые и линейно–изменяющиеся сигналы. При этом медианный фильтр подавляет импульсные выбросы исходного изображения, если длительность импульса составляет менее половины ширины окна. Так, например, если фрагмент изображения, попавший в окно фильтра, имеет вид (Рис.5.9,а), то после медианной фильтрации его опорный элемент принимает значение 39 вместо исходного 28 (Рис.5.9,б).
Для медианной фильтрации med{f} справедливо следующее правило вычисления, которое описывает суммирование константы со значением последовательности и умножение последовательности на некоторый коэффициент c:
med{c + f(к)} = с + med{f(k)};
и
med{cf(k)} = с med {f(k)}.
|
|
|
Рис.5.9. Иллюстрация медианной обработки фрагмента изображения |
Однако не является справедливым, что медианное значение суммы двух последовательностей равна сумме их медианных значений. Поэтому медианный фильтр является нелинейным. Медианные фильтры нередко применяются итеративно, причем обработка повторяется до тех пор, пока на профильтрованном изображении не прекратятся изменения.
5.4 Подчеркивание перепадов яркости и границ
Сглаживающие фильтры подавляют верхние частотные компоненты изображения, что приводит не только к уменьшению влияния шума, но и к потере мелких объектов изображения. Во многих задачах распознавания образов необходимо выделять границы объектов, подчеркивать перепады яркостей, селектировать мелкие объекты. Для реализации таких задач используются так называемые дифференциальные операторы. В таких операторах сумма элементов оконной функции h равна нулю, что свидетельствует о том, что в зонах изображения с постоянной яркостью они дают нулевой отклик. Дифференциальные операторы используются для вычисления градиента функции. Операция взятия градиента преобразует исходное изображение в новое с подчеркнутыми границами. Классическая функция градиента имеет вид
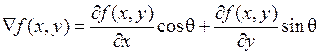 .
.
Абсолютное значение функции градиента определяется как
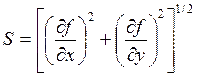 ,
,
а угол θ равен
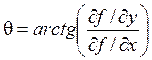 .
.
На практике применяют различные аппроксимации абсолютного значения градиента:
![]() ,
,
а для уменьшения затрат на вычисление градиента можно воспользоваться формулой
S= |Sх| + |Sу|
или
S = max (|Sx|, |Sy|),
а направление границы определять следующим образом θ = arctg (Sx/Sy).
Здесь Sx и Sy – приращения функции изображения по направлениям х и у, которые вычисляются по формулам:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.