У дискретного автомата без
памяти (комбинационной схемы) сигналы на выходах ![]() описываются логическими функциями выходов:
описываются логическими функциями выходов:
![]()
где n – число выходов
автомата; m – число входов автомата; ![]() - аргумент, соответствующий входному
сигналу.
- аргумент, соответствующий входному
сигналу.
Значения ![]() берутся в одни и те же
моменты времени, так как в случае автоматов без памяти можно пренебречь
временем задержки сигналов в логических элементах и временем срабатывания и
отпускания реле.
берутся в одни и те же
моменты времени, так как в случае автоматов без памяти можно пренебречь
временем задержки сигналов в логических элементах и временем срабатывания и
отпускания реле.
Процесс синтеза автоматов без памяти подразделяется на следующие этапы:
- блочный синтез (разбиение сложного автомата на подавтоматы);
- абстрактный синтез (формальное описание автомата и определение МДНФ логических функций выходов);
- структурный синтез (выбор элементной базы – системы элементов, приведение функций выходов к удобному для реализации в выбранной системе, разработка функциональных и принципиальных электрических схем автоматов);
Формальное описание автомата заключается в определении по словесному заданию числа входов и выходов, зависимостей между ними, построении таблиц соответствия либо карт Карно для функций выходов.
Для построения схемы автомата
на релейно-контактных элементах (РКЭ) целесообразно от МДНФ перейти к скобочным
формам и выделить группы вида ![]() , так как они легко реализуются соответствующим
соединением переключающих контактов.
, так как они легко реализуются соответствующим
соединением переключающих контактов.
При использовании элементов И (ИЛИ) с ограниченным числом входов нужно функцию выходов привести к такому виду, чтобы число операндов каждой операции И (ИЛИ) не превышало числа входов соответствующих элементов.
Если автомат строится на
микросхемах, характерных тем, что основные логические элементы имеют только
инверсные выходы, надо получить выражения функции ![]() с общим знаком отрицания. Это
необязательно для микросхем, в которые входят логические элементы с парафазным
(прямым и инверсным) выходом.
с общим знаком отрицания. Это
необязательно для микросхем, в которые входят логические элементы с парафазным
(прямым и инверсным) выходом.
Если число операндов некоторой операции И (ИЛИ) меньше числа входов имеющегося конъюнктора (дизъюнктора), то на неиспользуемые входы логического элемента необходимо подать постоянный сигнал “логическая 1” (“логический 0”). Для микросхем некоторых серий логической единице соответствует просто обрыв входа.
Пример 2.1. Схема свертки по mod3
целого положительного четырехразрядного двоичного числа ![]() принимает входные сигналы
принимает входные сигналы ![]() параллельным кодом.
Двухразрядный выходной код
параллельным кодом.
Двухразрядный выходной код ![]() является двоичным представлением остатка
от деления X на основание 3 (
является двоичным представлением остатка
от деления X на основание 3 (![]() – младшие разряды чисел).
– младшие разряды чисел).
Выполнить синтез этого автомата на следующих элементах:
а) реле с переключающими контактами;
б) логических элементах ЗИ, 2ИЛИ;
в) микросхемах серии К106;
г) микросхемах серии К172.
Решение. По заданному словесному описанию схемы
свертки можно построить таблицу соответствия (рисунок 2.7, а) и карты Карно для
функций выходов ![]() (рисунок
2.7, б), поскольку наборах 10…15
(рисунок
2.7, б), поскольку наборах 10…15 ![]() недоопределены. МДНФ этих функций имеют
вид:
недоопределены. МДНФ этих функций имеют
вид:
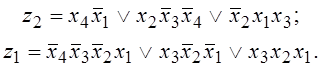
a)
|
N |
x4 |
x3 |
x2 |
x1 |
z2 |
z1 |
N |
x4 |
x3 |
x2 |
x1 |
z2 |
z1 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
8 |
1 |
0 |
0 |
0 |
1 |
0 |
|
|
1 |
0 |
0 |
0 |
1 |
0 |
1 |
9 |
1 |
0 |
0 |
1 |
0 |
0 |
|
|
2 |
0 |
0 |
1 |
0 |
1 |
0 |
10 |
1 |
0 |
1 |
0 |
– |
– |
|
|
3 |
0 |
0 |
1 |
1 |
0 |
0 |
11 |
1 |
0 |
1 |
1 |
– |
– |
|
|
4 |
0 |
1 |
0 |
0 |
0 |
1 |
12 |
1 |
1 |
0 |
0 |
– |
– |
|
|
5 |
0 |
1 |
0 |
1 |
1 |
0 |
13 |
1 |
1 |
0 |
1 |
– |
– |
|
|
6 |
0 |
1 |
1 |
0 |
0 |
0 |
14 |
1 |
1 |
1 |
0 |
– |
– |
|
|
7 |
0 |
1 |
1 |
1 |
0 |
1 |
15 |
1 |
1 |
1 |
1 |
– |
– |
|
б) |
|
|
в) |
|
|
г) |
|
Рис.2.7.
а) Чтобы реализовать эти функции на РКЭ, приведем их к виду:
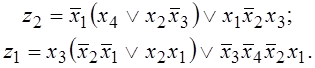
Составленная по этим выражениям схема автомата приведена на рисунке 2.7,в.
б) Если применять элементы ЗИ и ИЛИ, то функции выходов можно выразить как
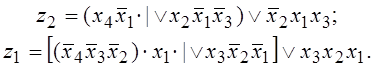
Реализация этих формул показана на рисунке 2.7,г.
в) При применении микросхем
серии К106 можно использовать различные представления ![]() с общим знаком инверсии, например:
с общим знаком инверсии, например:
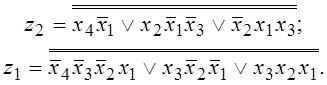
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.