Синтез дискретных автоматов без памяти. Синтез дискретных автоматов с памятью (Глава 2 учебного пособия "Основы электронной вычислительной техники и программирования"), страница 5

-  при одних и тех же последовательностях состояний входов формируются непротиворечивые последовательности состояний выходов, независимо от того, какое из псевдоэквивалентных принято за исходное внутреннее состояние.

Совместимым называют внутренние состояния, которым в таблицах переходов-выходов соответствуют столбцы, где в каждой строке непротиворечивы как состояния выходов, так и внутренние состояния. Они могут быть устойчивы при разных состояниях входов. Внутреннее состояние, объединяющее группу совместимых, устойчиво только тогда, когда устойчиво и любое из совместимых внутренних состояний. При объединении доопределяются не только выходы, но и переходы автомата.

После минимизации числа внутренних состояний определяется объем памяти

где   N – число внутренних состояний автомата; n – число элементов памяти;  - целое число, ближайшее к А сверху.

Рассмотрим примеры синтеза автоматов с памятью.

Пример 2.2.  Делитель частоты на 3 с импульсным входом x и выходом z описывается временными диаграммами (рисунок 2.10, а)

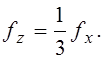
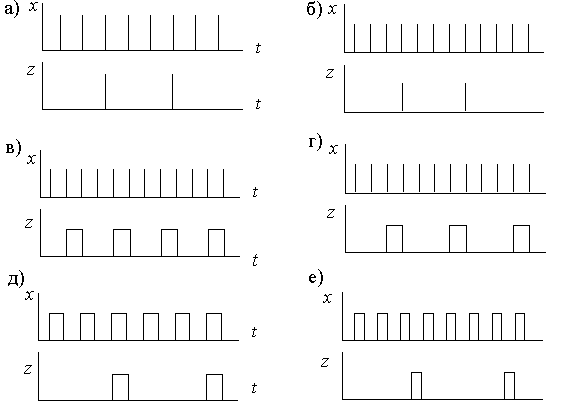
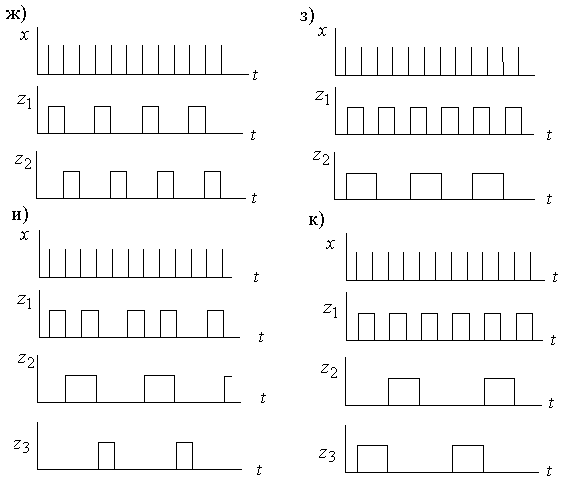
Рис.2.10.

Выполнить синтез автомата на многовходовых элементах И, ИЛИ. В качестве элементов памяти применить:

а) Т-триггеры;

б) JK-триггеры;

в) RS-триггеры.

Цепи сброса в исходное разработать при построении функциональной схемы.

Решение. По временным диаграммам легко определить, что исходное внутреннее состояние  делителя повторяется после каждого третьего импульса x. Если пренебречь длительностью x и временем переходных процессов в автомате, то автомат можно описать графом переходов, как показано на рисунке 2.11, а. По этому графу просто строится таблица переходов-выходов (рисунок 2.11, б). В схеме автомата должно быть два элемента памяти, так как 

.

Поскольку вход импульсный, кодировать внутренние состояния можно произвольно, например, натуральным двоичным кодом:

Тогда кодированная таблица переходов-выходов принимает вид, приведенный на рисунке 2.11, в, а перестроенная в карту Карно – на рисунке 2.11, г. Если отдельной картой Карно задать функцию z (рисунок 2.11,д), то ее МДНФ записывается как

                                                  (2.9)

Дальнейшие этапы синтеза зависят от типа применяемых триггеров.

а) Т-триггер изменяет свое внутреннее состояние при действии каждого импульса на счетном входе. Поэтому, если внутренние состояния в момент  и в момент  совпадают, функция возбуждения i-го триггера . Если , то .

Таким образом, воспользовавшись кодированной таблицей переходов, можно по парам , определяющим тип перехода i-го триггера, построить таблицу функций возбуждения входов . Такая таблица, выполненная в виде карты Карно, показана на рисунке 2.11,е, откуда функции возбуждений счетных входов элементов памяти

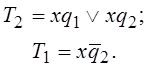                                           (2.10)

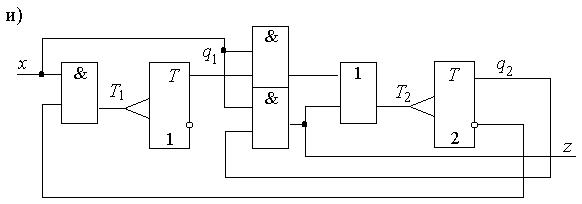
Рис.2.11.

Система функций (2.9), (2.10) реализуется схемой (рисунок 2.11,и). Для возврата в исходное состояние 00 у каждого триггера можно предусмотреть входы R раздельной установки в 0.

Такая схема делителя с RT-триггерами показана на рисунке 2.12, а.

б) Для определения функций возбуждения JK-триггеров, взятых в качестве элементов памяти делителя, надо воспользоваться таблицей, приведенной на рисунке 2.9,б, и кодированной таблицей переходов-выходов (рисунок 2.11,г). В зависимости от типа перехода  каждая клетка таблицы функций возбуждений заполняется нулевыми, единичными или безразличными значениями функций    , как показано на рисунке 2.10, ж. Эта таблица выполнена в виде карты Карно, откуда

                                 .                           (2.11)

Система функций (2.9), (2.11) реализуется схемой, приведенной на рисунке 2.12,б. Чтобы возвратить автомат в исходное состояние 00, у каждого триггера добавлено по одному входу , на которые подается сигнал сброса.

в) Аналогично происходит построение таблицы функций возбуждений элементов памяти типа RS-триггер (рисунок 2.11,з), при этом надо воспользоваться таблицей (смотри рисунок 2.9,а).