Синтез дискретных автоматов без памяти. Синтез дискретных автоматов с памятью (Глава 2 учебного пособия "Основы электронной вычислительной техники и программирования"), страница 6

Минимизируя, получаем:

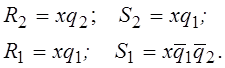                              (2.12)

Функциональная схема с цепями сброса в исходное, построенная по функциям (2.9), (2.12), показана на рисунке 2.12,в.

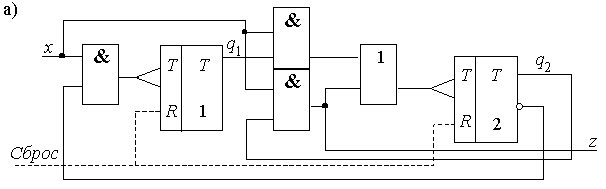
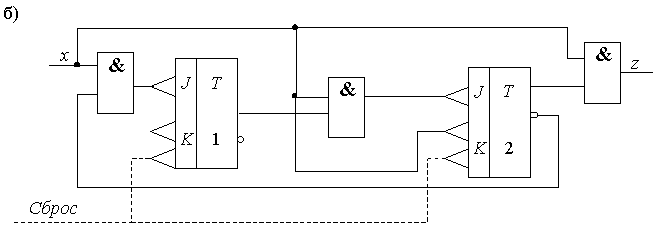
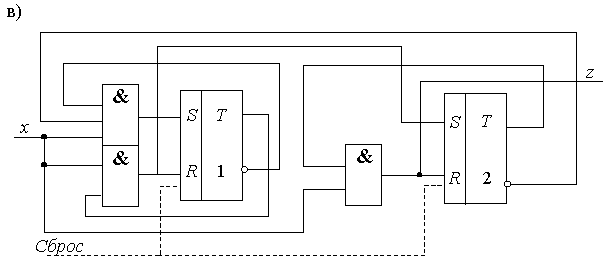
Рисунок 2.12

Пример 2.3. Делитель частоты на 3 с потенциальными входом x и выходом z описывается временными диаграммами (рисунок 2.10,д).

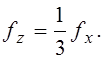
Синтезировать автомат, применив:

а) реле с переключающими контактами;

б) элементы памяти типа задержки и логические элементы серии К106;

в) RS-триггеры и логические элементы серии К106.

Решение. Анализ временных диаграмм показывает, что цикл работы устройства повторяется при исчезновении каждого третьего сигнала на входе х. Видно, что автомат имеет шесть внутренних состояний; в трех из них он находится при , в других трех – при . Этим он отличается от рассмотренного выше прототипа с импульсными входами, так как сейчас нельзя пренебрегать длительностью сигнала х. Граф переходов строится так, как показано на рисунке 2.13,а.

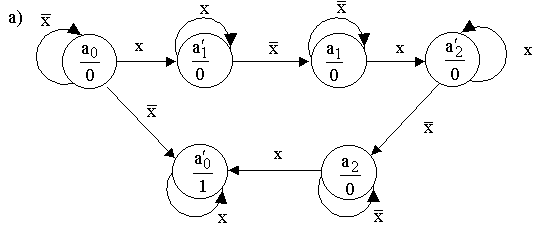
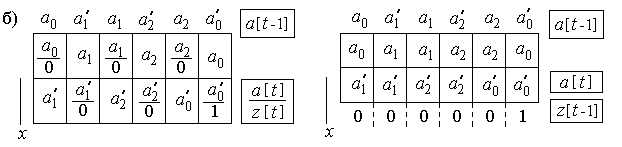
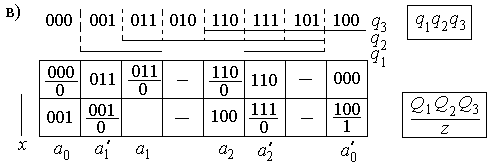
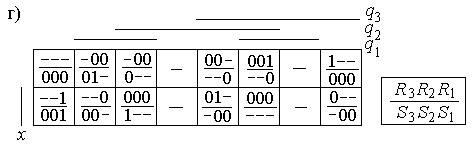
Рисунок 2.13.

Таблица переходов-выходов может быть построена двояко. Как общий случай таблица переходов-выходов представлена на рисунке 2.13,б. В клетках таблицы, соответствующих переходному процессу установки в новое внутреннее состояние, недоопределены состояния выходов. Можно дать следующие рекомендации. Если переход в новое внутреннее состояние не сопровождается сменой состояний выходов, то целесообразно не изменять выходные сигналы и во время перехода. Если же при переходе происходит изменение состояния какого-либо выхода, то в момент перехода сигнал на нем безразличен.

Как частный случай – автомат Мура, делитель описывается отмеченной таблицей переходов (рисунок 2.13, в).

Необходимое минимальное число элементов памяти:

Кодирование внутренних состояний автомата с темя элементами памяти можно выполнить по-разному. Один из способов, устраняющих состязания при действии х, – кодирование кодом Либау-Крейга:

Нетрудно видеть, что при этом память заполняется единицами, а затем нулями.

Кодированная таблица переходов-выходов принимает вид, показанный на рисунке 2.13,г. Отсюда можно найти, что:

                                                   (2.13)

а) Для вариантов условия задачи а) и б) элементы памяти – задержки. Поэтому таблица (смотри рисунок 2.13,г) задает и функции возбуждений . Если для упрощения работы каждую  задать картой Карно, то их МДНФ определяются как

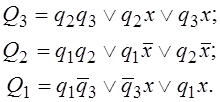                                    (2.14)

В случае РКЭ их можно представить в виде:

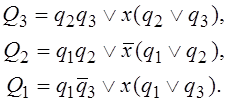                                   (2.15)

Реализация системы функций (2.13), (1.15) приведена на рисунке 2.14,б, где для уменьшения числа контактов применены диоды.

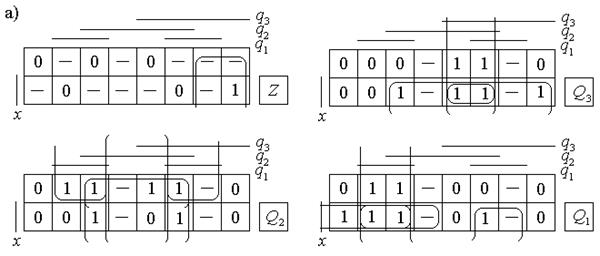
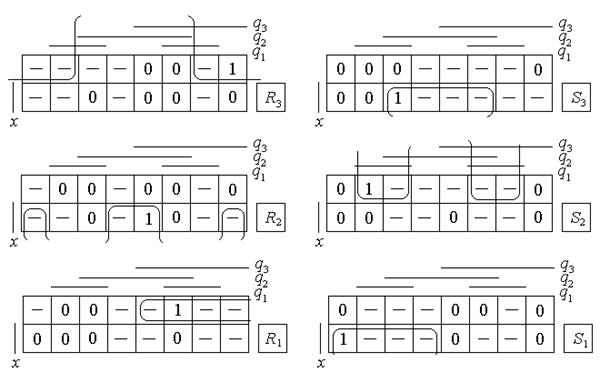
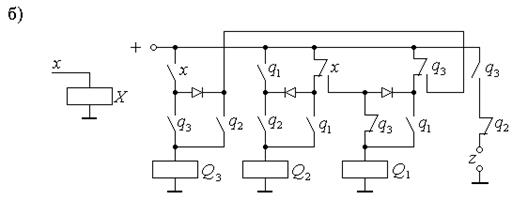
Рис. 2.14.

б) В случае микросхем серии К106 функции возбуждений элементов памяти типа задержки можно представить как:

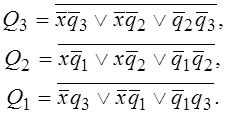                                 (2.16)

Если использовать элементы 2И-НЕ с расширением по ИЛИ и расширители, то схема, реализующая систему функций (2.13), (2.16), может быть построена так, как показано на рисунке 2.15,а.

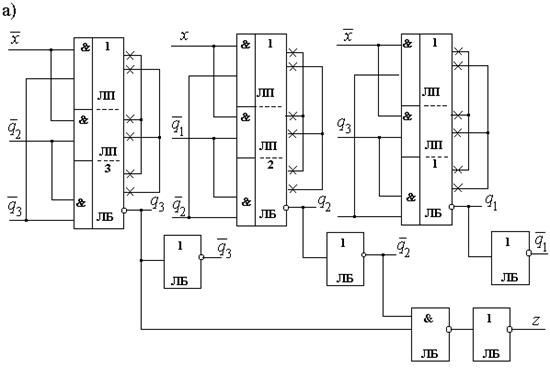
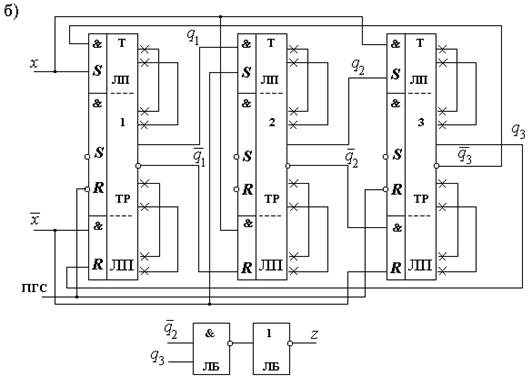
Рис.2.15.

в) Применение RS-триггеров делает необходимым построение таблиц функций возбуждений (i=1,2,3) (смотри рисунок 2.13,д). Минимизируя с помощью карт Карно (рисунок 2.14,а), имеем

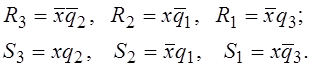                          (2.17)

Использование расширительных входов триггеров и расширителей по ИЛИ позволит представить в совмещенном изображении схему, реализующую функции (2.13), (2.17), как показано на рисунке 2.15,б. Здесь, в отличии от двух предыдущих случаев, предусмотрен сброс в исходное путем подачи нулевого сигнала на инверторные входы  всех триггеров одновременно.

 Пример 2.4  Выполнить синтез делителя частоты на 3 с потенциальным входом х, используя импульсный прототип, описанный в примере 2.2.

Решение. Если задачу решить, синтезируя делитель на 3 с импульсным входом и памятью на двух JK-триггерах, а затем, получив функцию выходов z (2.9) и функции  (2.11), использовать микросхемы (элементы И-НЕ и JK-триггеры с входной логикой), то схема автомата принимает вид, показанный на рисунке 2.16.

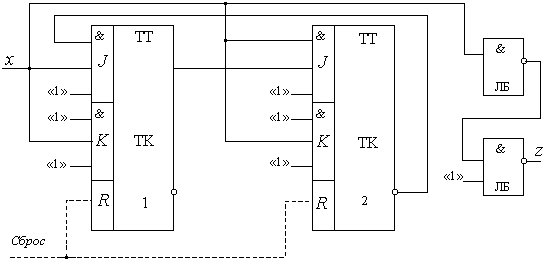
Рис. 2.16.