Анализ дискретных автоматов без памяти. Анализ дискретных автоматов с памятью на триггерах (Глава 2 учебного пособия "Основы электронной вычислительной техники и программирования")

2.11  Анализ дискретных автоматов без памяти

Целью анализа дискретных автоматов без памяти (комбинацион­ных схем) является определение условий их функционирования, в результате чего выявляются наборы комбинаций аргументов (весо­вые состояния), на которых значение функций выходов равно 1 (рабочие состояния).

Процесс анализа дискретных автоматов без памяти подразделя­ется на следующие этапы:

- по функциональной схеме определяются входы и выходы авто­мата;

- вписываются логические функции выходов в аналитической форме, которая зависит от типа системы логических элементов;

- определяются ДНФ этих функций;

- от ДНФ переходят к форме представления функций выходов которая удобна для дальнейшего построения таблиц соответствия, например, находят СДНФ или задают функции выходов картами Карно;

- строится таблица соответствия,

Следует отметить, что если анализируемый автомат имеет сложную структуру, то его целесообразно разбить на несколько более простых, описание которых не составляет труда, а затем произве­сти анализ.

При анализе схем, выполненных на РКЭ, необходимо определить, какую структуру имеет заданный автомат.

Схемы, имеющие структуру класса П, анализируются сравнительно  просто - записываются логические функции, описывающие контактную часть.

Если адаптируемый автомат (комбинационная схема) имеет структуру класса Н, тогда целесообразно преобразовать ее в структуру  класса П любым из известных способов, а затем записать ло­гическую функцию выходов.

Если дискретный автомат выполнен на интегральных микросхемах необходимо учитывать, что принципиальная и функциональная электрические схемы отличается лишь количеством информации (нумерация входных и выходных выводов, маркировка элементов и линий связи и т.д.). Поэтому функция выходов определяется по прин­ципиальной электрической схеме.

Пример 2.5. Анализировать схему автомата, представленную на рис.2.17,а.

Решение. Сначала необходимо убедиться в отсутствии обратных связей. В данном примере их нет, так как ни одно реле не имеет собственных контактов в цепях возбуждения своих обмоток, кроме этого, отсутствуют и перекрестные обратные связи. Реле А и В управляют обмоткой D, но реле D никакого влия­ния на реле A и B не оказывает.

Особенностью данной схемы является то, что сигнал на обмот­ке D формируется нормальной, а на обмотке E (выходе) инверс­ной структурой. Поэтому

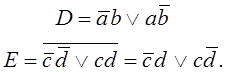
Учитывая отсутствие обратных связей и приравнивая , получаем:

Полученное выражение является СДНФ функции выхода, и по нему можно легко построить таблицу соответствия или карту Карно.

Если входам присвоить веса , то результат может быть представлен в виде:

Этот автомат представляет собой сумматор по модулю 2, выполненный на РКЭ.

В алгебре Жегалкина функция выхода автомата будет иметь вид:

.

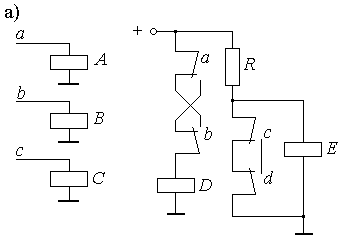
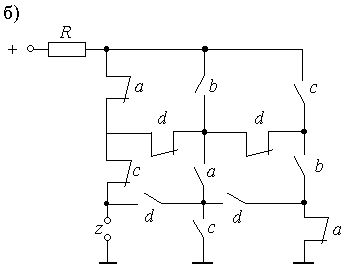
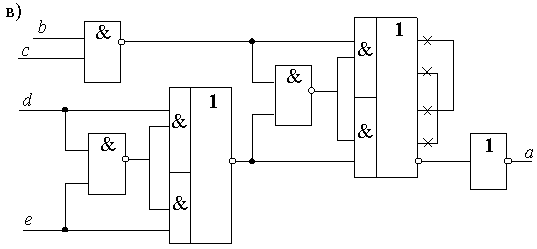
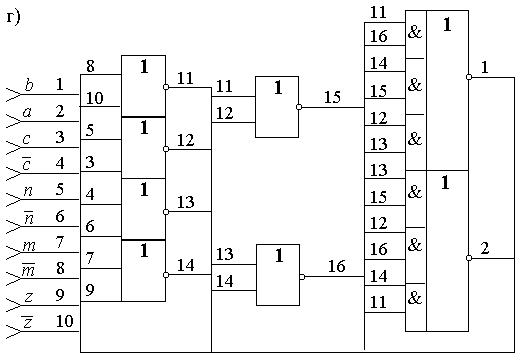
Рис.2.17.

Пример 2.6. Определить состояния входов автомата, при которых выходной сигнал, формируемый  схемой,  приведенной  на рисунке 2.17,б, равен 1.

Решение. Предлагаемая для анализа схема представляет собой структуру класса Н смешанного типа.

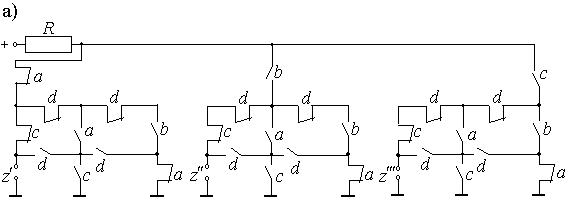
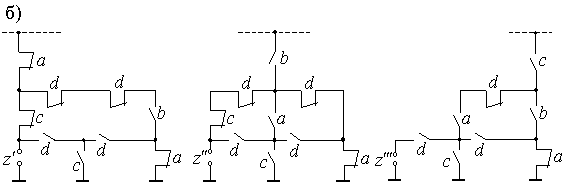
Выполним решение этой задачи, разложив схему (смотрите рисунок 2.17,б) по начальным элементам.

Рис.2.18.

Результат разложения приведен на рисунке 2.18,а.

Таким образом, получается схема как бы с тремя выводами , причем .

Применим формулы разложения для конъюнкции к схеме на рис.2.18,а: в левой схеме замыкающий контакт реле А разры­ваем и шунтируем размыкающий, в средней схеме замыкающий кон­такт реле 5  шунтируем, в правой замыкающий контакт реле В шунтируем, а размыкающий - разрываем.

Теперь получаем структуры класса П, в которых можно выделить нормальные и инверсные группы (рисунок 2.18,б ):

           

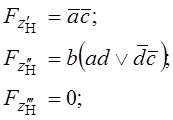
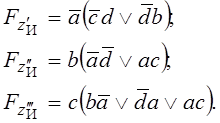
Запишем значение для z, учитывая, что структура смешанная:

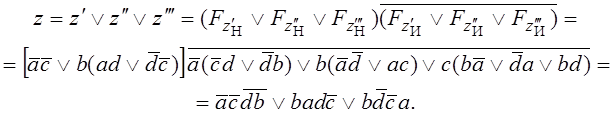
По этому выражению легко построить карту Карно (рис.2.18,в) или таблицу соответствия.

Присвоив аргументам веса: , можно представить функцию выхода в виде

.

Решение этой задачи можно выполнись иначе. Учитывая, что мостиковыми являются только контакты реле D, схему можно заменить эквивалентной ей схемой (рисунок 2.18, г), которая представляет собой реализацию следующих очевидных соотношений:

,

где F – логическая функция, описывающая контактную часть структуры (см. рисунок 2.17,б).

Таким образом, получается схема как бы с двумя выходами  и , причем в .

Применим формулы разложения для конъюнкции к схеме, приве­денной на рисунке 2.18,а: в левой схеме размыкающие контакты реле D разрываем, замыкающие – шунтируем, а в правой – наоборот.

Получим две структуры класса П, в  которых можно выделять нормальные и инверсные группы:

           

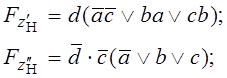
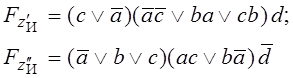
Отсюда

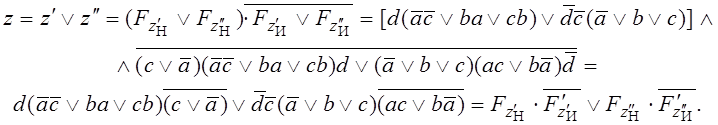
Через  и  обозначены логические функции, описывающие контактные группы, инверсные соответствующим выходам и не содержащие частей, входящих в нормальные группы.

После преобразования ДНФ функции выхода  будет иметь вид:

Таким образом, выполнив решение задачи двумя различными способами, убеждаемся в правильности результата.

Пример 2.7. Выполнить анализ схемы, приведенной на рис.2.17,в.

Решение. Следуя правилу изображения схем цифровой техники определяем, что входами автомата являются b, c, d, e выходом – a. Это схема с совмещенным изображением логических элементов.