Анализ дискретных автоматов без памяти. Анализ дискретных автоматов с памятью на триггерах (Глава 2 учебного пособия "Основы электронной вычислительной техники и программирования"), страница 3

Пример 2.9. Выполнить анализ автомата, схема которого представлена на рис. 2.19,а.

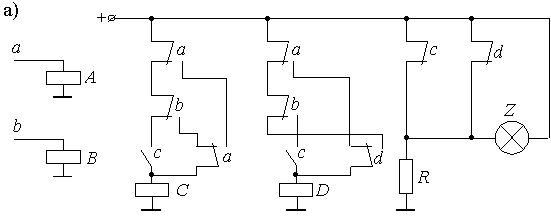
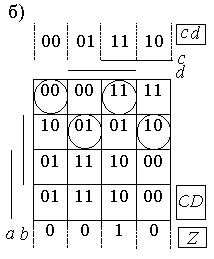
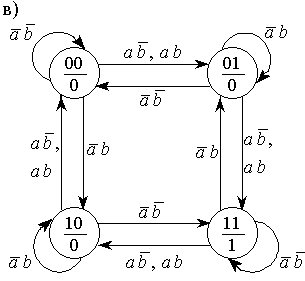
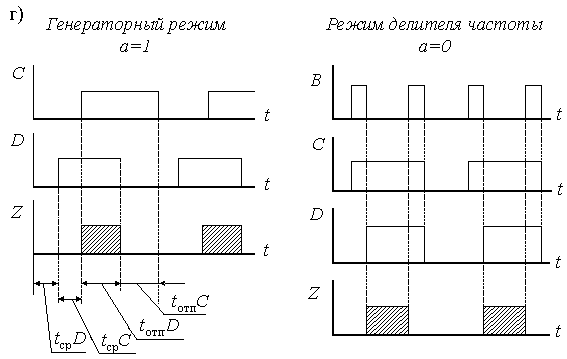
Рис.2.19.

Решение. Из схемы видно, что приемными элементами, воспринимающими входные сигналы , являются обмотки реле A и B, а выход этого автомата – клеммы лампочки . Нужно отметить, что лампочка  включена параллельно контактной цепи , т.е. автомат имеет следующую функцию выхода:

В цепях возбуждения обмотки реле С находятся как собственные контакты, так и контакты реле D. Аналогично выполнены и цепи возбуждения реле D.

Таким образом, элементами памяти являются реле С и D, задержки в которых существенны.

Определив входы, выходы и элементы памяти автомата, можно записать функции возбуждений:

Функции возбуждений записаны в виде ДНФ, и, учитывая, что элементами памяти являются задержки, они тождественны функциям переходов автомата.

Так как функция выходов зависит лишь от аргументов  и , анализируемый автомат является автоматом Мура, и для него можно строить отмеченную кодированную таблицу переходов. Полное число внутренних состояний этого автомата равно , поэтому такая таблица имеет четыре столбца.

Число строк в таблице определяется числом возможных комби­наций входных сигналов и равно четырем. Для простоты заполнения таблицы значениями функций С и D представим ее в виде карты Карно (рис.2.19,б) и занесем туда единицы и нули в соответствии с импликантами ДНФ.

Функция выхода  равна единице только в одном случае, при . Отмеченная кодированная таблица представлена на рисунке 2.19,б.

Отметим кружками те клетки таблицы, в которых комбинации состояний элементов памяти совпадают с комбинациями, указанными над столбцами т.е. устойчивые состояния автомата.

Отсутствие устойчивых состоянии в третьей и четвертой стро­ках означает, что автомат имеет генераторный режим без состяза­ний элементов памяти: замкнутый цикл переходов через неустойчи­вые состояния выполняется до тех пор, пока .

Частота появления выходного сигнала  определяется вре­менем срабатывания и отпускания реле.

Из таблицы видно, что при  выходной сигнал равен 1 при каждой нечетной паузе между сигналами на входе .

Таким образом, автомат работает при  как генератор, а при  – как делитель частоты на два, причем длительность выходного сигнала равна длительности паузы между сигналами на входе .

Граф переходов и временные диаграммы работы схемы представ­лены на рис.2.19,в,г.

Пример 2.10. Выполнить анализ автомата, схема которого пред­ставлена на рис.2.20,а.

Решение. По графическому изображению схемы определяем, что  и  – входы автомата, а  и  – выходы. Очевид­но, что обратными связями охвачены четвертый и пятый логические элементы, поэтому задержки в них являются существенными.

Представим каждый из них в виде последовательно включенных безынерционного логического элемента и элемента задержки (рис.2.20,б). Обозначив входы и выходы задержек, запишем функ­ции выходов и функции переходов, совпадающие с функциями возбуж­дений, в виде

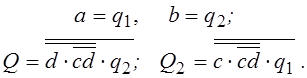
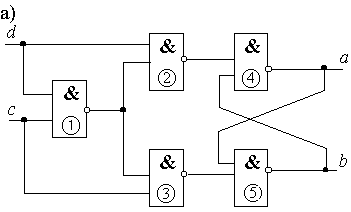
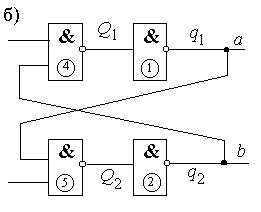
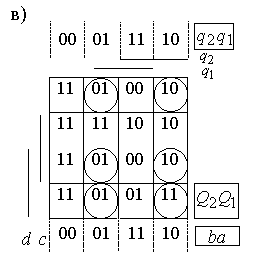
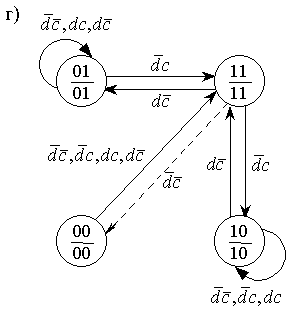
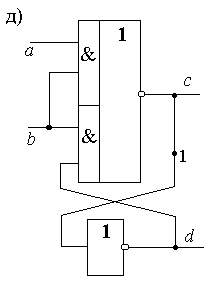
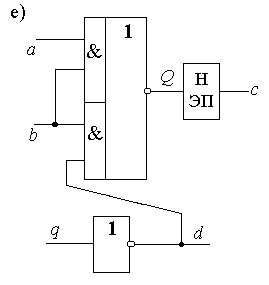
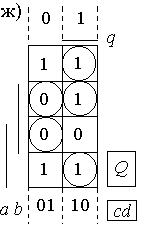
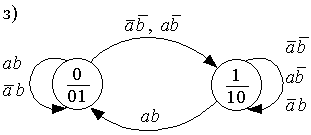
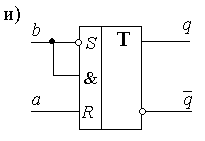
Рис.2.20.

По виду функции выходов определяем, что анализируемый автомат – автомат Мура. Для него строится отмеченная таблица переходов. Функции переходов представим в виде ДНФ:  и по импликантам заполним карту Карно; таблица переходов примет вид рисунок 2.20,в. Устойчивые состояния отметим в таблице кружками и построим граф переходов (рисунок 2.20,г).

Рассматривая таблицу и граф переходов, можно сделать выводы:

-  автомат имеет лишь два устойчивых внутренних состояния: 01 и 10, при этом состояния выходов противоположны;

-  переход из одного устойчивого состояния в другое совершается через неустойчивое внутреннее состояние 11 без состязаний элементов памяти и с кратковременным  появлением единиц на обоих выходах;

-  неустойчивое внутреннее состояние 00 практически недостижимо, так как из-за состязания элементов памяти переход из 11 под действием комбинации  будет происходить не в 00, а в одно из устойчивых состояний.