Анализ дискретных автоматов без памяти. Анализ дискретных автоматов с памятью на триггерах (Глава 2 учебного пособия "Основы электронной вычислительной техники и программирования"), страница 2

Прослеживая пути прохождения входных сигналов, записываем функцию выхода:

,

где .

Подставив  в выражение для а, имеем:

По полученным импликантам ДНФ, присвоив аргументам веса , легко заполнить карту Карно, опре­делив затем номера наборов, на которых функция выходов равна единице:

На остальных наборах входных сигналов выходной сигнал равен нулю.

Приведем ДНФ функции выходов к СДНФ, домножив каждую конъюнкцию ДНФ на дизъюнкцию отсутствующего в ней аргумента и его инверсии:

Совпадение результатов говорит о правильности решения задачи.

Пример 2.8. Определить состояния входов схемы (см. рисунок 2.17,г) при которых выходные сигналы равны единице.

Решение. На рис.2.17,г приведена функциональная схема с линиями групповой связи (кодовыми шинами) и штепсельным разъемом. Для анализа схемы вначале нужно определить, какие гнезда разъема соответствуют  входу и выходу автомата.

Если некоторый проводник штепсельного разъема соединен с выходом хотя бы одного логического элемента, то он является вы­водом автомата.

Проводник разъема, соединенный только с входами логических элементов, является входом автомата.

Прослеживая связи в схеме, определяем, что выходами являются  и , а входами –  Таким образом, информация на входы поступает парафазным кодом.

Обозначим выходы логических элементов символом , где  – номер проводника в кодовой шине. Получаем:

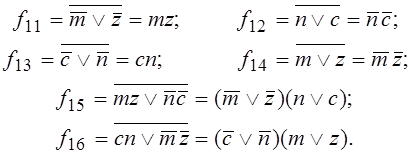
Отсюда значения функций выходов  и  соответственно равны

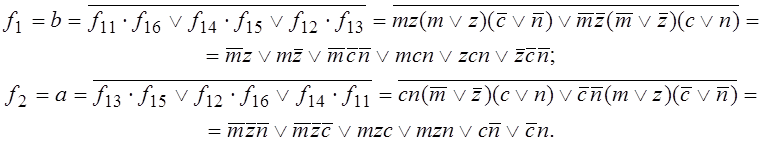
Приведем ДНФ функций выходов  и  к СДНФ, домножив каждую конъюнкцию ДНФ на дизъюнкцию отсутствующего в ней аргумента и его инверсии.

Присвоив аргументам веса  получаем:

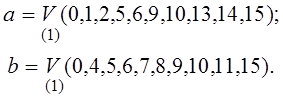
Аналогичный результат получаем, если карту Карно заполнить по импликантам полученных ДНФ для выходов  и .

2.12  Анализ дискретных автоматов с памятью на задержках

Задачей анализа автоматов с памятью является определение функций переходов, описывающих закон изменения внутренних состояний, и функций выходов по принципиальным электрическим схе­мам.

Конечным результатом анализа автоматов с памятью является получение таблиц переходов - выходов, по которым затем легко построить граф переходов для заданного автомата.

Анализ автомата с памятью состоит из следующих этапов:

-  по принципиальной схеме устанавливается тип логических элементов;

-  выявляются элементы памяти, входы и выходы автомата;

-  строится функциональная схема автомата;

-  по функциональной схеме определяются логические функции вводов и функции возбуждений;

-  в зависимости от типа элементов памяти по функциям возбуж­дений олределяются функции переходов;

-  аналитические выражения функций переходов и выходов приво­дятся к виду, удобному для построения таблиц; обычно это ДНФ или СДНФ;

-  строятся таблицы переходов - выходов и при необходимости графы переходов и временные диаграммы.

Если дискретный автомат с памятью построен на бесконтактных логических элементах или РКЭ, то в его схеме трудно либо невозможно выделить группы элементов, образующие триггеры известного типа. Поэтому один из этапов анализа на задержках – выявление элементов памяти. Элементами памяти будут те логические элементы, которые образуют существенные задержки в работе автомата.

Существенными называются задержки, которые определяют характер переходов и образуются в элементах, включенных в контур обратной связи.

При анализе дискретных автоматов с памятью, выполненных на логических элементах, существенными принято считать задержки в элементах, расположенных непосредственно перед точками съема сигналов обратных связей,

В схемах, выполненных на релейно-контактных элементах, существенные задержки будут в тех реле, в цепях возбуждения обмоток которых включены собственные контакты этих реле или имеют место перекрестные обратные связи.

Отличительной особенностью анализа автоматов с памятью на задержках является то, что функции переходов совпадают с функциями возбуждения.